| BeschreibungAcadem Arithmetic progressions along a knotted loop.svg |
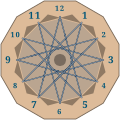
English: Called regular dodecagons, a few polygons have twelve sides within the image. Consider two regular dodecagons sharing their center and all their vertices. If they are different, one of them is convex, the other is stellated. A side of any of them is a diagonal of the other.
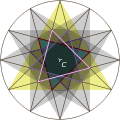
The hours are numbered from 1 to 12. There is an one-to-one correspondence between the sides of the clock and these integers, written beside the twelve sides. Twelve hairpin bends can be also numbered from 1 to 12, along an imaginary decagonal race track, the plan of which is on the clock face. Such an object is called a knot in mathematics. We meet no intersection along this loop, but forty-eight bridges. Every straight line crosses eight other parts, passing alternatively under and above. We see the same knot on another version. This knot imparts an information: a stellated polygon is really a polygon. In other words, it is a closed polygonal chain: the twelve sides of the star can be traced without lifting the pencil.
For example, if we start at the bend numbered one, we come back to the same bend numbered one after covering the whole track, exactly after five turns around the center. This rotation can be seen as the "transformation into the identical one", in other words: a rotation of which the angle is zero modulo 360 degrees. By passing from a bend of the track to the next one, we turn 150 degrees around the center: 5 × 30° = 150°. And 12 × 150° = 5 × 360° = 0° modulo 360°. Provided that their centers coincide, and that their angles are equal modulo 360 degrees, several rotations are identical.
By turning clockwise, we pass through the twelve bends: 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8. Whatever the integer from which we start, up to congruence modulo 12, we pass through the terms of an arithmetic progression with common difference 5 or 7, depending on the sense of rotation, either clockwise or the inverse sense. The common differences –5 and +7 are equivalent: –5 = +7 modulo 12.
If it is now nine o'clock, it will be noon in three hours. Up to congruence modulo 12, the sequence (9; 0; 3; 6) is an arithmetic progression with common difference +3 or –9. The hairpin bends numbered 9, 0, 3, 6, are the vertices of a square. Up to similarity, there is only one regular quadrilateral: the square, denoted by {4,1} in Schläfli notation, not {12,3}. One of the following notations denotes a regular dodecagon: {12,1} for a convex one, otherwise {12,5}.
Français : Appelés des dodécagones réguliers, quelques polygones ont douze côtés dans l’image. Considérons deux dodécagones réguliers partageant leur centre et tous leurs sommets. S’ils sont différents, l’un d’eux est convexe, l’autre est étoilé. Un côté de l’un est une diagonale de l’autre.
Les heures sont numérotées de 1 à 12. Il existe une correspondance biunivoque entre les côtés de l’horloge et ces nombres entiers, inscrits près des douze côtés. Douze virages en épingle à cheveux peuvent aussi être numérotés de 1 à 12, le long d’une piste de course décagonale imaginaire, dont le plan est sur le cadran de l’horloge. Un tel objet s’appellle un nœud en mathématiques. Nous ne rencontrons aucune intersection le long de cette boucle, mais quarante-huit ponts. Chaque ligne droite croise huit autres parties, en passant alternativement en dessous et au-dessus. On voit le même nœud dans une autre version. Ce nœud donne une information : un polygone étoilé est bien un polygone. Autrement dit, il s’agit d’une ligne brisée fermée : les douze côtés de l’étoile peuvent être tracés sans lever le crayon.
Par exemple, si nous partons du virage numéro un, nous revenons au même virage numéro un après avoir parcouru toute la piste, exactement après cinq tours autour du centre. Cette rotation peut être considérée comme la “transformation à l’identique”, autrement dit : une rotation dont l’angle est nul modulo 360 degrés. En passant d’un virage de la piste au suivant, nous tournons de 150 degrés autour du centre : 5 × 30° = 150°. Et 12 × 150° = 5 × 360° = 0° modulo 360°. Pourvu que leurs centres coïncident, et que leurs angles soient égaux modulo 360 degrés, plusieurs rotations sont identiques.
En tournant dans le sens des aiguilles d’une montre, nous passons par les douze virages: 1, 6, 11, 4, 9, 2, 7, 12, 5, 10, 3, 8. Quel que soit le nombre entier duquel nous partons, à la congruence près modulo 12, nous passons par les termes d’une progression arithmétique de raison 5 ou 7, selon le sens de la rotation, soit dans le sens horaire, soit dans le sens inverse. Les raisons –5 et +7 sont équivalentes : –5 = +7 modulo 12.
S’il est maintenant neuf heures, il sera midi dans trois heures. À la congruence près modulo 12, la suite (9; 0; 3; 6) est une progression arithmétique de raison +3 ou –9. Les virages numérotés 9, 0, 3, 6, sont les sommets d’un carré. Aux similitudes près, il existe un seul quadrilatère régulier : le carré, noté {4,1} en notation de Schläfli, et non {12,3}. L’une des notations suivantes désigne un dodécagone régulier : {12,1} s’il est convexe, sinon {12,5}. |