Krawattenknoten

Mit dem Krawattenknoten wird die Schlaufe der Krawatte erzeugt, die für den mechanischen Halt am Hals sorgt. Der Krawattenknoten lässt sich einteilen in die Standardknoten, wie den Windsor- oder den Pratt-Knoten, und die Sonderformen, wie den Onassis-Knoten, den invertierten Knoten oder den Kreuzknoten.

Bei einigen Ausführungen befindet sich unterhalb des Knotens eine kleine Furche bzw. Falte, im Fachjargon „dimple“ (engl. für Grübchen, Vertiefung) genannt. Für diese besondere Ausprägung finden sich Gegner und Befürworter. Es bleibt dem Geschmack und der Vorliebe des Krawattenträgers überlassen, ob eine Krawattenfalte zum guten Aussehen beiträgt oder nicht.

Standardknoten

	symmetrische Knoten		asymmetrische Knoten
Naht zeigt zum Hals	klein groß	Halber Windsorknoten () Windsorknoten	klein groß	Four-in-Hand * Victoria * Cavendish (*)
Naht zeigt nach außen	klein groß	Pratt (Nicky ) Andreas Balthus ; Hannoveraner ()	klein groß	Kleiner Knoten Kelvin Plattsburgh () Grantchester
()* Der Knoten ist selbstlösend, () d. h., er zerfällt vollständig, wenn das schmale Ende nach oben aus dem Knoten gezogen wird. () (Dies ist genau dann der Fall, wenn der Knoten mit bzw. endet.) (*) Es gibt eine selbstlösende Variante des Knotens

Als Standardknoten werden Knoten bezeichnet, bei denen das breite Ende der Krawatte ohne Torsion um das schmale Ende geschlungen wird. Dabei entsteht eine verstellbare Schlaufe und das schmale Ende kann durch den Knoten hin- und hergezogen werden.

Die Mathematiker Thomas Fink und Yong Mao haben systematisch alle auf diese Weise bindbaren Krawattenknoten untersucht und insgesamt 85 Knotenvarianten für Krawatten mit üblicher Länge beschrieben. Die Mehrzahl dieser Knotenvarianten ergibt allerdings Knoten, die unförmig sind oder sich schlecht zuziehen lassen. Somit ist die Menge der in der Praxis brauchbaren Knoten überschaubar und beinhaltet jeweils nur wenige Varianten einer Knotenklasse (vgl. Abschnitt Systematische Klassifizierung der Standardknoten).^[1]

Die vier Klassiker

Nebenstehende Abbildungen sind seitenverkehrt, also wie das eigene Spiegelbild.

Four-in-Hand

Auch als einfacher Knoten bezeichnet.
Der Ursprung des Namens four-in-hand („Vier in der Hand“) ist nicht eindeutig geklärt. Eine Theorie besagt, dass Kutscher ihre Zügel mit diesem Knoten versahen. Andere gehen davon aus, dass die Mitglieder des Londoner Four-in-Hand-Clubs diesen Krawattenknoten salonfähig machten.

Halber Windsorknoten

Fälschlich auch oft „einfacher Windsorknoten“ genannt.
Es ist nicht bekannt, ob der halbe Windsorknoten aus dem Windsorknoten hervorging oder unabhängig davon entstand. Vereinzelt wird dieser Knoten auch als halber englischer oder türkischer Knoten bezeichnet.

Selbstlösende Variante

Etwas asymmetrischer als die andere Variante.

Windsorknoten

Auch oft „doppelter Windsorknoten“ genannt.
Der Name ist auf den Duke of Windsor zurückzuführen, der diesen Knoten allerdings nicht selbst erfand. In seinem Buch A Family Album (Cassell, London, 1960) schreibt er, man habe den in den Vereinigten Staaten erfundenen Knoten irrtümlich nach ihm benannt, da er stets dicke Krawattenknoten getragen habe. Diese seien jedoch durch das dicke Tuch seiner Krawatten und nicht durch einen besonders komplexen Knoten entstanden. Teilweise findet sich auch die Bezeichnung englischer Knoten.

Variante mit zwei Ringbewegungen

Diese Variante mit zwei Ringbewegungen führt zu einem etwas schmaleren, aber dennoch vollen Knoten. Sie eignet sich für die meisten Krawatten und ist daher sehr beliebt.

Variante: Persischer Knoten

Der Persische Knoten ist ein Windsorknoten mit einer Ring- und einer Diagonalbewegung. Dadurch wird ein Knoten erzielt, der nicht selbstlösend ist.

Pratt-Knoten

Der Pratt-Knoten wurde vom US-Handelskammer-Mitglied Jerry Pratt erfunden. Gelegentlich wird der Knoten auch als Shelby-Knoten bezeichnet: nachdem Pratt dem Fernsehmoderator Donald Shelby seinen Knoten beigebracht hatte, trug dieser ihn häufig in seinen Sendungen.

Selbstlösende Variante („Nicky“)

Diese Variante weist etwas höhere Formstabilität auf.

Weitere

Sankt-Andreas-Knoten

Balthus-Knoten

Hannoveranerknoten

Benannt nach den Hannoveranern.
Der Hannoveranerknoten ist eine Erweiterung des Windsorknotens.

Selbstlösende Variante

Victoria-Knoten

Variante: Prinz-Albert-Knoten

Dabei wird im letzten Schritt des Victoria-Knotens das breite Ende unter beiden waagerechten Streifen hindurchgeführt. Es entsteht ein Knoten, der an einen Blütenkelch erinnert, ähnlich dem Kreuzknoten.

Cavendish-Knoten

Der Cavendish-Knoten entsteht durch Hintereinanderausführung zweier Four-in-Hand-Knoten.

Selbstlösende Variante

Kleiner Knoten

Auch als orientalischer Knoten bezeichnet.
Dieser Knoten ist abschließender Bestandteil sämtlicher Standardknoten. Er erfreut sich in China großer Beliebtheit. Um einen ansehnlichen Knoten zu erreichen, benötigt man eine Krawatte aus dickem Tuch.

Kelvin-Knoten

Benannt nach Lord Kelvin.
Wie beim Victoria-Knoten ist auch hier eine Variante möglich: im letzten Schritt lässt sich das breite Ende unter beiden waagerechten Streifen durchschieben. Der Kelvin-Knoten ist der kleinste Knoten, bei dem das möglich ist.

Plattsburgh-Knoten

Benannt nach der Stadt Plattsburgh in den USA.

Selbstlösende Variante

Grantchester-Knoten

Benannt nach dem Ort Grantchester bei Cambridge.
In Deutschland ist aber auch die Bezeichnung Manhattan-Knoten üblich.

Systematische Klassifizierung der Standardknoten

Klassifizierung der einzelnen Bewegungen
Ausgangslage
waagerechte Bewegung
Zentrumsbewegung	Diagonalbewegung
Zentrumsbewegung	Ringbewegung

Abschluss (=Kleiner Knoten)		-	-

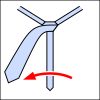
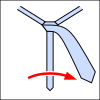
Während des Bindens eines Krawattenknotens bleibt das schmale Ende der Krawatte stets in der gleichen Position, und das breite Ende wird bewegt. Dabei treten diese Muster auf:

Das breite Ende befindet sich links des schmalen Endes
Das breite Ende befindet sich rechts des schmalen Endes
Das breite Ende befindet sich in der Schlinge

Dabei lässt sich der letzte Zustand auch als Übergang zwischen den beiden ersten interpretieren. Betrachtet man jeweils nur die Bewegungen, die das breite Ende von einer Seite des schmalen Endes auf die andere Seite bewegen, so findet man, dass in jeder Situation genau drei Bewegungen möglich sind:

waagerecht über das schmale Ende (bzw. darunter hindurch)
durch die Schlinge auf die andere Seite
durch die Schlinge zurück zur Ausgangsposition

In nebenstehender Tabelle sind die möglichen Bewegungen für alle Ausgangslagen aufgelistet. Da am Ende jedes Standardknotens der kleine Knoten gebildet wird, genügt es zur vollständigen Beschreibung eines Knotens, die Bewegungen bis zum kleinen Knoten aufzulisten. Der halbe Windsorknoten beispielsweise ergibt sich aus der Bewegungsfolge

waagerecht – diagonal (+ Kleiner Knoten),

der Windsorknoten aus

diagonal – waagerecht – diagonal (+ Kleiner Knoten)

Knoten mit der gleichen Anzahl an Zentrums- und waagerechten Bewegungen haben ähnliche Form und Größe. Daher empfiehlt es sich, die Standardknoten nach diesen Quantitäten zu klassifizieren. Knoten der gleichen Klasse unterscheiden sich dann nur in der Reihenfolge der Bewegungen und in der Art der Zentrumsbewegungen (Diagonal- oder Ringbewegung). Die Größe eines Knotens definieren wir wie folgt:

der Kleine Knoten hat Größe 3
eine waagerechte Bewegung erhöht die Größe um 1
eine Zentrumsbewegung erhöht die Größe um 2

Durch Ausprobieren zeigt sich, dass normale Krawatten zu kurz sind für Knoten mit Größe 10 und mehr. Folgendes Diagramm klassifiziert die Knoten bis Größe 9, wobei $\gamma$ für die Anzahl der Zentrumsbewegungen und $h$ für die Größe steht. Eine waagerechte Linie symbolisiert eine waagerechte Bewegung, eine diagonale Linie eine Zentrumsbewegung. Da diese sich in Diagonal- und Ringbewegungen gliedern, treten die diagonalen Linien paarweise auf.

Durch einfache Überlegung ergibt sich, dass die Größe der (im Diagramm blau markierten) Knoten, bei denen die Naht zum Hals zeigt, stets gerade ist, und dass andererseits die Größe der Knoten mit Naht nach außen immer ungerade ist.

Umgekehrt kann man also aus der Parität der Größe eines Knotens die Orientierung der Naht ableiten. Allerdings ist es auch möglich, Knoten mit ungerader Größe so zu binden, dass die Naht nach innen zeigt (und umgekehrt). Dazu wird vor dem Binden nur das breite Ende verdreht.^[2]

In der Praxis erweisen sich die mit X markierten Knoten als unästhetisch, so dass noch 13 Klassen von brauchbaren Knoten übrigbleiben. Zu einer Klasse gehören alle Knoten, die aus der gleichen Anzahl an Zentrumsbewegungen $\gamma$ und waagrechten Bewegungen $w$ (ohne den kleinen Knoten als Abschluss) bestehen. Die Anzahl der Reihenfolgen dieser Bewegungen beträgt ${\tbinom {w+\gamma }{\gamma }}$ , zusätzlich gibt es für jede der $\gamma$ Zentrumsbewegungen unabhängig die Ring- oder Diagonalbewegung. Die Anzahl der Knoten in einer Klasse beträgt daher $2^{\gamma }\cdot {\tbinom {w+\gamma }{\gamma }}$ .

Es ergibt sich folgende Tabelle:

Klasse Nummer	Anzahl der Knoten in der Klasse $2^{\gamma }\cdot {\tbinom {w+\gamma }{\gamma }}$	Namen der Knoten	waagerechte Bewegungen $w$	Zentrums- bewegungen $\gamma$	Größe $h=w+2\gamma +3$
1	1	Kleiner Knoten	0	0	3
2	1	Four-in-Hand	1	0	4
3	1	Kelvin	2	0	5
4	1	Victoria	3	0	6
X	jeweils 1	(keine gut aussehenden Knoten)	4, 5, 6	0	7, 8, 9
5	2	Nicky, Pratt	0	1	5
6	4	Halber Windsor + 03 Varianten	1	1	6
7	6	Sankt Andreas + 05 Varianten	2	1	7
8	8	Cavendish + 07 Varianten	3	1	8
9	10	Grantchester + 09 Varianten	4	1	9
10	4	Plattsburgh + 03 Varianten	0	2	7
11	12	Windsor + 11 Varianten	1	2	8
12	24	Hannoveraner + 23 Varianten	2	2	9
13	8	Balthus + 07 Varianten	0	3	9
Summe	85

Sonderknoten

Onassis-Knoten

Der Onassis-Knoten wurde vom griechischen Reeder Aristoteles Onassis getragen.

Als Basis des Onassis-Knotens dient der Four-in-Hand oder ein anderer kleiner Knoten, über den das breite Ende übergeworfen wird.

Kreuzknoten

Christensen-Knoten

Diese Variante des Cavendish ist nur für schmale Krawatten geeignet.

Im letzten Schritt wird das breitere Ende unter beiden waagerechten Streifen hindurch geführt, so dass auf dem Knoten zwei sich überkreuzende Streifen sichtbar bleiben.

Invertierte Knoten

Bei Standardknoten mit ungerader Größe ist die Naht des schmalen Endes vom Körper weg gerichtet. Betrachtet man die fertig gebundene Krawatte von der Rückseite, so ist diese Naht also nicht sichtbar. Das führt zu der Idee, die Rückseite des Standardknotens als neuen Knoten zu verwenden: Es ergibt sich aus jedem Standardknoten ungerader Größe ein neuer Knoten, indem beim Binden von Anfang an die beiden Enden vertauscht werden, also das schmale Ende um das breite Ende geschlungen, und die fertig geknotete Krawatte um 180° gedreht wird. Es empfiehlt sich, die Krawatte in der Hand zu binden und erst danach anzulegen.

Invertierte Knoten sind kleiner als die zugehörigen Standardknoten, da das schmale Ende weniger Material zum Volumenaufbau beiträgt. Die benötigte Länge der Krawatte ist aber in etwa gleich.

Eine Auswahl invertierter Knoten:

Atlantik-Knoten

Dies ist ein invertierter Pratt-Knoten.

Diagonal-rechts-Knoten

Dabei handelt es sich um einen invertierten Kelvin-Knoten.

Der Name rührt von der diagonalen kleinen Schlaufe auf der – vom Träger aus gesehen – rechten Seite her.

Merowinger-Knoten

Dieser Knoten wurde nach der Matrix-Figur Merowinger benannt und wird ursprünglich auch als Ediety bezeichnet.

Der Knoten ist ein invertierter Knoten mit der Bewegungsfolge

Ring – waagerecht – Ring – waagerecht – Ring (+ Kleiner Knoten)

und hat somit Größe 11. Eine extralange Krawatte ist daher für den Merowinger-Knoten unverzichtbar.

Galerie

Windsor
Halber Windsor
Four-in-Hand
Sankt-Andreas-Knoten
Kleiner Knoten
Pratt

Siehe auch

Binden einer Fliege (Querbinder).

Literatur

Thomas Fink, Yong Mao: Die 85 Methoden, eine Krawatte zu binden. Piper, München 2006. ISBN 3-492-24739-3
Thomas Fink, Yong Mao: Tie knots, random walks and topology (PDF; 197 kB). in: Physica A 276. Amsterdam 2000, 109–121. ISSN 0378-4371

Einzelnachweise

↑ Thomas Fink, Yong Mao: Tie knots, random walks and topology (PDF; 197 kB). in: Physica A 276. Amsterdam 2000, 109–121. ISSN 0378-4371
↑ Der Kentknoten. Spotn.de, 19. Oktober 2007, archiviert vom Original am 11. September 2010; abgerufen am 24. August 2014.

Weblinks

Commons: Krawattenknoten – Sammlung von Bildern, Videos und Audiodateien

Encyclopedia of Tie Knots von Thomas Fink
Krawattenknoten.org mit Anleitungen für diverse Krawattenknoten, Krawattenpflege und Dresscodes
Ausführliche Anleitungen diverser Knoten als pdf (englisch) – Seite von Lord Whimsy
Zusammenfassung von 20 verschiedenen Krawattenknoten mit dazugehörigen Lernvideos

Weitere Knoten

Alex Krasny: Eldredge. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Alex Krasny: Trinity. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Alex Krasny: Cape. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Patrick Novotny: Novotny. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Eliot Truelove: Truelove. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Eliot Truelove: Ellie. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Sidewinder. In: YouTube. Abgerufen am 6. April 2013 (englisch).
Fancy Braided. In: YouTube. Abgerufen am 6. April 2013 (englisch).
The Left Ostridge. In: YouTube. Abgerufen am 6. April 2013 (englisch).

[finkmao-1] Thomas Fink, Yong Mao: Tie knots, random walks and topology (PDF; 197 kB). in: Physica A 276. Amsterdam 2000, 109–121. ISSN 0378-4371

[kent-2] Der Kentknoten. Spotn.de, 19. Oktober 2007, archiviert vom Original am 11. September 2010; abgerufen am 24. August 2014.

[1]

[2]

Krawattenknoten

Inhaltsverzeichnis