Dilatation (Geometrie)

Zur Definition einer Dilatation: $\delta (g)|g$

Als Dilatation bezeichnet man in der Geometrie eine Kollineation einer affinen Ebene oder eines affinen Raumes, mit der Eigenschaft, dass

• jede Gerade auf eine zu ihr parallele Gerade abgebildet wird.

Dilatationen sind spezielle Affinitäten. Genauer gilt:

• Eine von der Identität verschiedene Dilatation ist entweder eine zentrische Streckung (mit einem Fixpunkt) oder eine Parallelverschiebung (ohne Fixpunkt).

affine Versionen des Satzes von Desargues.
Oben: großer Satz,
unten: kleiner Satz

In der synthetischen Geometrie nennt man zentrische Streckungen auch Homothetien. Sie haben dort einen direkten Bezug zur affinen Form des großen Satzes von Desargues (siehe Bild). Parallelverschiebungen nennt man auch Translationen. Sie haben Bezug zur affinen Form des kleinen Satzes von Desargues. Die Hintereinanderausführung zweier Translationen ist immer auch eine Translation. Die analoge Aussage gilt für Homothetien nicht. Zum Beispiel ist die Hintereinanderausführung zweier Punktspiegelungen eine Translation und keine Homothetie. Alle Dilatationen bilden eine Gruppe und alle Translationen eine Untergruppe davon. Bettet man die zugrunde liegende Ebene/Raum in eine projektive Ebene/Raum ein, so wird aus einer Dilatation eine Zentralkollineation mit der Fern-Gerade/-Hyperebene als Achse. Genauer: aus einer Translation bzw. Homothetie wird dann eine Elation bzw. Homologie, je nachdem, ob das Zentrum auf der Achse liegt oder nicht.

In einem euklidischen Raum lässt sich

• eine Streckung am Nullpunkt durch $\ {\vec {x}}\to c{\vec {x}}\ ,\ c\neq 0,$
• eine Translation durch $\ {\vec {x}}\to {\vec {x}}+{\vec {v}}\$

beschreiben. Während Translationen Streckenlängen invariant lassen, verlängert oder verkürzt eine zentrische Streckung Strecken um denselben Faktor. In der oberen Figur des zweiten Bildes wird das blaue Dreieck durch eine zentrische Streckung an dem Punkt $Z$ auf das grüne Dreieck abgebildet. In der unteren Figur geht das blaue Dreieck durch eine Translation in das (kongruente) grüne Dreieck über. Dilatationen gehören zu den Ähnlichkeitsabbildungen.

Man beachte: Achsenaffinitäten sind keine Dilatationen.

Definitionen

Die Definition der linearen Algebra ist für desarguesche affine Ebenen äquivalent zur Definition der synthetischen Geometrie, für nichtdesarguesche Ebenen ist nur die synthetische Definition sinnvoll und insofern eine Verallgemeinerung. Es gibt auch für höherdimensionale affine Geometrien rein geometrische Definitionen, die aber dann äquivalent zur Definition der linearen Algebra sind.

Lineare Algebra

Sei $K$ ein Körper oder Schiefkörper, $V$ ein Vektorraum bzw. Linksvektorraum über $K$, dessen Dimension über $K$ mindestens 2 ist, ${\mathcal {A}}$ ein affiner Raum über $K$, dessen Verbindungsvektoren $V\,$ bilden. Dann heißt eine Affinität $\alpha \colon {\mathcal {A}}\rightarrow {\mathcal {A}}$ Dilatation, wenn ein Skalar $a\in K\setminus \{0\}$ existiert, so dass für zwei Punkte $P,Q\in {\mathcal {A}}\,$ stets ${\overrightarrow {\alpha (P)\alpha (Q)}}=a\cdot {\overrightarrow {PQ}}\,$ gilt. Der durch die Dilatation eindeutig bestimmte Skalar $a$ heißt Streckfaktor von $\alpha$. Für $a=1$ ist $\alpha$ eine Translation.

Synthetische Geometrie

Sei ${\mathcal {A}}$ eine affine Ebene. Eine Kollineation, also eine geradentreue Bijektion $\alpha \colon {\mathcal {A}}\rightarrow {\mathcal {A}}$ heißt Dilatation, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist:

1. Jede Gerade $g$ der Ebene ist zu ihrer Bildgeraden $\alpha (g)$ parallel.
2. Die Fortsetzung von $\alpha$ im projektiven Abschluss von ${\mathcal {A}}$ ist eine projektive Perspektivität, bei der die Ferngerade eine Fixpunktgerade ist.

Dilatationsgruppen

Zu einer mindestens zweidimensionalen affinen Geometrie heißt

• die Gruppe der Dilatationen auf ${\mathcal {A}}$ Dilatationsgruppe $\Delta ({\mathcal {A}})$ von ${\mathcal {A}}$,
• die Gruppe der Dilatationen mit einem festen Fixpunkt $Z\in {\mathcal {A}}$ (verallgemeinerte) Streckungsgruppe $\Delta _{Z}({\mathcal {A}})$ mit Zentrum $Z$,
• die Gruppe der Dilatationen ohne Fixpunkt zusammen mit der Identität Translationsgruppe ${\mathcal {T}}({\mathcal {A}})$.

Eigenschaften

Allgemein

• Jede Dilatation ist eine Affinität.
• Eine Affinität oder Kollineation auf einer mindestens zweidimensionalen affinen Geometrie ist genau dann eine Dilatation, wenn jede Gerade parallel zu ihrer Bildgeraden ist.
• Hat eine Dilatation mehr als einen Fixpunkt, dann ist sie die identische Abbildung.
• Eine Dilatation ist durch die Angabe der Bildpunkte für zwei verschiedene Punkte des Raumes eindeutig bestimmt.
• Bei einer nichtidentischen Dilatation mit einem Fixpunkt $Z$ sind genau die Geraden durch $Z$ Fixgeraden.
• Bei einer nichtidentischen Translation $\tau \in {\mathcal {T}}({\mathcal {A}})$ sind genau die Parallelen zu der Verbindungsgeraden $P\,\tau (P)$ Fixgeraden, wobei $P\in {\mathcal {A}}$ ein beliebiger Punkt ist.
• In einer affinen Geometrie, die das affine Fano-Axiom erfüllt, ist jede Punktspiegelung eine Dilatation.

Struktur der Dilatationsgruppen

• Die Translationsgruppe ist ein Normalteiler der Dilatationsgruppe $\left({\mathcal {T}}({\mathcal {A}})\triangleleft \Delta ({\mathcal {A}})\right)$.
• Falls zu zwei Punkten $X,Y\in {\mathcal {A}}$ eine Translation $\tau \in {\mathcal {T}}({\mathcal {A}})$ existiert, die $X$ auf $Y$ abbildet $\left(\tau (X)=Y\right)$, dann sind die verallgemeinerten Streckungsgruppen $\Delta _{X}({\mathcal {A}}),\Delta _{Y}({\mathcal {A}})<\Delta ({\mathcal {A}})$ in der Dilatationsgruppe konjugierte Untergruppen – es gilt dann $\tau \Delta _{X}({\mathcal {A}})\tau ^{-1}=\Delta _{Y}({\mathcal {A}})$ – und also isomorph zueinander.

Desarguessche Räume

• In einem $n$-dimensionalen affinen Raum ($n\geq 2$) über einem Schiefkörper $K$ gilt:

1. Eine Dilatation $\alpha$ ist genau dann eine Translation, wenn der ihr zugeordnete Streckungsfaktor $a=1$ ist, ansonsten hat sie einen Fixpunkt $Z$ und es gilt $\alpha \in \Delta _{Z}({\mathcal {A}})$.
2. Die Translationsgruppe ist ein kommutativer Normalteiler der Dilatationsgruppe und als Gruppe isomorph zum $K$-Linksvektorraum der Verbindungsvektoren $\left(({\mathcal {T}}({\mathcal {A}}),\circ )\cong (K^{n},+)\right)$.
3. Die Streckungsgruppen zu beliebigen Zentren sind zueinander und zur multiplikativen Gruppe des Schiefkörpers isomorph $\left((\Delta _{X}({\mathcal {A}}),\circ )\cong (\Delta _{Y}({\mathcal {A}}),\circ )\cong (K^{\ast },\cdot )\right)$. Dabei wird bei dem Isomorphismus zur multiplikativen Gruppe des Schiefkörpers jeder Streckung ihr Streckfaktor zugeordnet.
4. Die Dilatationsgruppe ist das innere semidirekte Produkt der Translationsgruppe mit einer beliebigen Streckungsgruppe: $\Delta ({\mathcal {A}})\cong {\mathcal {T}}({\mathcal {A}})\cdot \Delta _{Z}({\mathcal {A}})$.
5. Insbesondere lässt sich jede Dilatation $\alpha$ eindeutig als Verkettung einer Streckung um den fest gewählten Ursprung $O\in {\mathcal {A}}$ mit einer anschließenden Translation darstellen.
6. Die Dilatationsgruppe ist isomorph zu einem äußeren semidirekten Produkt: $(\Delta ({\mathcal {A}}),\circ )\cong (K^{n},+)\times _{\theta }(K^{\ast },\cdot )$. Die Operation $\theta$ von $K^{\ast }$ auf $K^{n}$ ist dabei durch die Linksmultiplikation mit den Streckfaktoren gegeben.
7. Ist $K$ ein endlicher Körper mit $q$ Elementen, dann enthält die Dilatationsgruppe $q^{n}\cdot (q-1)$ Elemente.

Affine Translationsebenen

• In einer affinen Translationsebene, deren Koordinatenbereich der Linksquasikörper $K$ und deren Schiefkörper der spurtreuen Endomorphismen der Translationsgruppe $S=\operatorname {Kern} (K)$ ist, gilt:

1. Zu jeder Dilatation $\alpha$ existiert eine Konstante $a\in S^{\ast }$, so dass für beliebige Punkte $P,Q\in {\mathcal {A}}$ stets ${\overrightarrow {\alpha (P)\alpha (Q)}}=a\cdot {\overrightarrow {PQ}}$ gilt. Diese Konstante wird wie im desarguesschen Fall als Streckfaktor der Dilatation bezeichnet. Eine Dilatation $\alpha$ ist genau dann eine Translation, wenn ihr Streckfaktor $a=1$ ist, ansonsten hat sie einen Fixpunkt $Z$ und es gilt $\alpha \in \Delta _{Z}({\mathcal {A}})$.
2. Die Translationsgruppe ist ein kommutativer Normalteiler der Dilatationsgruppe und als Gruppe isomorph zum $S$-Linksvektorraum der Verschiebungen $\left(({\mathcal {T}},\circ )\cong (K^{2},+)\right)$.
3. Die Streckungsgruppen zu beliebigen Zentren sind zueinander und zur multiplikativen Gruppe von $S=\operatorname {Kern} (K)$ isomorph $\left((\Delta _{X}({\mathcal {A}}),\circ )\cong (\Delta _{Y}({\mathcal {A}}),\circ )\cong (S^{\ast },\cdot )\right)$. Dabei wird bei dem Isomorphismus zur multiplikativen Gruppe $S^{\ast }$ jeder Streckung ihr Streckfaktor zugeordnet.
4. Die Dilatationsgruppe ist das innere semidirekte Produkt der Translationsgruppe mit einer beliebigen Streckungsgruppe: $\Delta ({\mathcal {A}})\cong {\mathcal {T}}({\mathcal {A}})\cdot \Delta _{Z}({\mathcal {A}})$.
5. Insbesondere lässt sich jede Dilatation $\alpha$ eindeutig als Verkettung einer Streckung um den fest gewählten Ursprung $O\in {\mathcal {A}}$ mit einer anschließenden Translation darstellen.
6. Die Dilatationsgruppe ist isomorph zu einem äußeren semidirekten Produkt: $(\Delta ({\mathcal {A}}),\circ )\cong (K^{2},+)\times _{\theta }(S^{\ast },\cdot )$. Die Operation $\theta$ von $S^{\ast }$ auf $K^{2}$ ist dabei durch die Linksmultiplikation mit den Streckfaktoren gegeben.
7. Ist der Quasikörper $K$ endlich und demnach ein $r$-dimensionaler Vektorraum über seinem Kern, einem endlichen Körper mit $q$ Elementen, dann enthält die Dilatationsgruppe $q^{2r}\cdot (q-1)$ Elemente.

Längen, Winkel, Volumina

Ebenen

• Ist in einer affinen Inzidenzebene ${\mathcal {A}}$ eine Orthogonalitätsrelation zwischen den Geraden gegeben, dann bleibt die Orthogonalität bei einer Dilatation $\alpha$ erhalten: Sind $g,h$ Geraden der Ebene, dann gilt $g\perp h\;\Leftrightarrow \;\alpha (g)\perp \alpha (h)$. Dies bleibt auch dann richtig, wenn die Orthogonalität isotrope Geraden ($g\perp g$) zulässt.
• In einer präeuklidischen Ebene gilt:

1. Das Bild eines rechtwinkligen Koordinatensystems $S=(O,E_{1},E_{2})$ ist wieder ein rechtwinkliges Koordinatensystem $\alpha (S)=(\alpha (O),\alpha (E_{1}),\alpha (E_{2}))$. Die Orthogonalitätskonstanten bezüglich $S$ und $\alpha (S)$ sind gleich.
2. Ist ${\mathcal {A}}$ eine präeuklidische Ebene mit Quadraten und $S$ ein kartesisches Koordinatensystem, dann ist auch $\alpha (S)$ kartesisch.
3. Jede Dilatation ist kreistreu: Das Bild eines Kreises ist ein Kreis.
4. Das Bild einer Längenklasse ist eine Längenklasse: Sind die Pfeile $(P_{1},Q_{1})$ und $(P_{2},Q_{2})$ gleich lang, dann gilt das auch für ihre Bildpfeile $(\alpha (P_{1}),\alpha (Q_{1}))$ und $(\alpha (P_{2}),\alpha (Q_{2}))$ unter einer Dilatation $\alpha$.
5. Ist der Streckfaktor einer Dilatation 1 oder −1, dann bildet diese Dilatation sogar jede Längenklasse auf sich selbst ab. Mit anderen Worten: Genau die Translationen und die Punktspiegelungen sind längentreue Dilatationen.

• In einer euklidischen Ebene oder allgemeiner in einer angeordneten, frei beweglichen Ebene mit einem Längenmaß für Strecken und einem (orientierten) Winkelmaß gilt:

1. Das (orientierte) Winkelmaß ist invariant unter jeder Dilatation.
2. Für das Verhältnis der Länge einer Strecke zur Länge der Bildstrecke gilt: $|\alpha (P)\alpha (Q)|:|PQ|=|a|$, dabei sind $P,Q\in {\mathcal {A}}$ verschiedene Punkte der Ebene, $a$ der Streckfaktor der Dilatation $\alpha$. Insbesondere sind genau die Translationen und Punktspiegelungen längentreue Dilatationen, und bei jeder Dilatation bleiben die Verhältnisse von zwei beliebigen Streckenlängen erhalten.
3. Ist die Ebene orientiert, so ist jede Dilatation orientierungserhaltend.

Beachte, dass für Ebenen über nicht archimedisch geordneten Körpern die Streckfaktoren $a$ auch „unendliche“ Zahlen sein können.

Räume mit Skalarprodukt

In einem mindestens zweidimensionalen affinen Raum ${\mathcal {A}}$ über einem Teilkörper $K$ der reellen Zahlen $\mathbb {R}$, in dessen $K$-Vektorraum der Verbindungsvektoren $V$ ein Skalarprodukt $\langle \cdot ,\cdot \rangle \colon V\times V\rightarrow \mathbb {R}$ erklärt ist, gilt:

1. Das Skalarprodukt von Verbindungsvektoren ändert sich für eine Dilatation $\alpha$ immer um den gleichen Faktor, es gilt genauer: $\langle {\overrightarrow {\alpha (P)\alpha (Q)}},{\overrightarrow {\alpha (R)\alpha (S)}}\rangle =a^{2}\cdot \langle {\overrightarrow {PQ}},{\overrightarrow {RS}}\rangle$ mit dem Streckfaktor $a$ von $\alpha$.
2. Ist $K$ ein starrer Teilkörper der reellen Zahlen, dann gilt sogar eine Art Umkehrung: Ist $f\colon {\mathcal {A}}\rightarrow {\mathcal {A}}$ eine Abbildung, die die Eigenschaft $\langle {\overrightarrow {f(P)f(Q)}},{\overrightarrow {f(R)f(S)}}\rangle =a^{2}\cdot \langle {\overrightarrow {PQ}},{\overrightarrow {RS}}\rangle$ für beliebige Punkte $P,Q,R,S\in {\mathcal {A}}$ und jedes Skalarprodukt auf $V$ mit derselben Konstanten $a\in K^{\ast }$ erfüllt, dann ist $f$ eine Dilatation von ${\mathcal {A}}$ mit dem Streckfaktor $a$ oder $-a$.
3. Das mit Hilfe des Skalarprodukts definierte (nicht orientierte) Winkelmaß ist invariant unter jeder Dilatation.
4. Die mit Hilfe des Skalarproduktes definierte (Quadrat-)Norm jedes Verbindungsvektors vervielfacht sich um den Betrag des Streckfaktors einer Dilatation: $\|{\overrightarrow {\alpha (P)\alpha (Q)}}\|_{2}=|a|\cdot \|{\overrightarrow {PQ}}\|_{2}$.
5. Insbesondere sind genau die Translationen und Punktspiegelungen längentreue Dilatationen und bei jeder Dilatation bleiben die Verhältnisse von zwei beliebigen Streckenlängen erhalten.

   

   Zur Winkelorientierung: $A,B,C\in {\mathcal {A}}$ bilden ein Dreieck, $B$ ist das Zentrum der Drehung um das Winkelmaß $w(\angle ABC)$, bei der der Strahl $BA^{+}$ durch das zu messende Winkelfeld auf $BC^{+}$ gedreht wird.

6. Ist auf dem Raum ein mit der Norm verträgliches, translationsinvariantes, $\sigma$-additives Volumenmaß $\operatorname {vol}$ gegeben, dann gilt für messbare Teilmengen $M\subset {\mathcal {A}}:\,|\operatorname {vol} (\alpha (M))|=|a|^{n}\cdot |\operatorname {vol} (M)|$.
7. Das Bild eines rechtwinkligen Koordinatensystems unter einer Dilatation ist wieder ein rechtwinkliges Koordinatensystem.
8. In einem orientierten affinen Raum der Dimension $n\geq 2$ über einem angeordneten Teilkörper der reellen Zahlen gilt:

• Eine Dilatation ist genau dann orientierungstreu, wenn ihr Streckfaktor positiv oder die Dimension $n$ des Raumes eine gerade Zahl ist, sonst kehrt sie die Orientierung um.
• Der Betrag des orientierten Winkelmaß $w(\angle ABC)$ eines gerichteten Winkels $\angle ABC$ bleibt bei jeder Dilatation erhalten. Vergleiche die Abbildungen rechts und in der Einleitung! Berücksichtigt man das Vorzeichen des Winkels, dann gilt genauer $w(\angle \alpha (A)\alpha (B)\alpha (C))=\operatorname {sgn}(a)^{n}\cdot w(\angle ABC),$ wobei $\operatorname {sgn}$ die Vorzeichenfunktion ist.
• Ist auf dem Raum ein mit der Norm verträgliches, orientiertes, translationsinvariantes, $\sigma$-additives Volumenmaß $\operatorname {vol}$ gegeben, dann gilt für messbare, orientierte Teilmengen $M\subset {\mathcal {A}}:\,\operatorname {vol} (\alpha (M))=a^{n}\cdot \operatorname {vol} (M)$.

Bildkonstruktion, Eindeutigkeit und Existenz

Beim Hauptfall sind vier verschiedene, komplanare Punkte $A_{1},A_{2},B_{1},B_{2}$ vorgegeben oder aus den Vorgaben konstruierbar, die ein nichtentartetes Trapez, aber kein Parallelogramm bilden. Das Trapez darf auch „überschlagen“ sein. Die nicht parallelen Trapezseiten schneiden einander im Zentrum $Z$ der Dilatation.

Im Folgenden ist ${\mathcal {A}}$ stets eine mindestens zweidimensionale affine Geometrie. Die Abbildungen zu den Konstruktionen in diesem Abschnitt können auch räumlich verstanden werden: Die (bis zu vier) Vorgabepunkte liegen stets in einer gemeinsamen Ebene der Geometrie, in der auch das Zentrum liegt, sofern es existiert. Zu Vorgaben, die nicht in einer gemeinsamen Ebene liegen, existiert keine Dilatation. Soll nun zu einem weiteren Punkt $C_{1}$ der Bildpunkt konstruiert werden, so liegen wieder alle an der Konstruktion beteiligten Punkte in einer Ebene, die allerdings nicht die durch die Vorgabepunkte bestimmte sein muss. Insgesamt spielen sich alle hier beschriebenen „Konstruktionen“ in einem höchstens dreidimensionalen affinen Teilraum der Geometrie ${\mathcal {A}}$ ab.

Ein Fixpunkt vorgegeben

Ist ein Punkt-Bildpunktpaar $A_{1},A_{2}$ und ein Fixpunkt $Z$ gegeben, dann existiert nur dann eine Dilatation $\alpha$ mit $\alpha (A_{1})=A_{2};\alpha (Z)=Z$, wenn

1. die Punkte $Z,A_{1},A_{2}$ kollinear und verschieden sind oder
2. $A_{1}=A_{2}\neq Z$ ist oder
3. $A_{1}=A_{2}=Z$ ist.

Im 2. Fall existiert genau eine Dilatation mit der geforderten Eigenschaft: Die Identität des Raumes. Im 3. Fall existiert mindestens die Identität, die die geforderte Eigenschaft hat, im Allgemeinen gibt es weitere zentrale Dilatationen mit der geforderten Eigenschaft, im 1. Fall existiert höchstens eine Dilatation mit der geforderten Eigenschaft. Ist ${\mathcal {A}}$ eine desarguesche Geometrie, so existiert eine solche Dilatation, ist ${\mathcal {A}}$ eine affine Translationsebene, dann existiert sie genau dann, wenn $Z,A_{1},A_{2}$ kommensurabel sind. Die Konstruktion kann so erfolgen, wie weiter unten beim „Hauptfall“ beschrieben. Vergleiche auch die Abbildung rechts.

Zwei Punkt-Bildpunktpaare vorgegeben

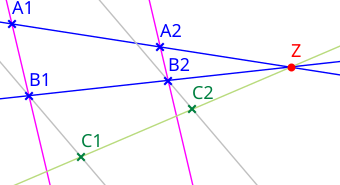
Sind $A_{1},A_{2},B_{1},B_{2}$ vier verschiedene Punkte der Geometrie, dann existiert nur in folgenden Fällen eine Dilatation $\alpha$ mit $\alpha (A_{1})=A_{2};\alpha (B_{1})=B_{2}:$

1. Die vier Punkte bilden ein Parallelogramm $A_{1}B_{1}B_{2}A_{2}$ oder
2. sie bilden ein – eventuell auch überschlagenes – nicht entartetes Trapez $A_{1}B_{1}B_{2}A_{2}$ mit $A_{1}B_{1}\parallel A_{2}B_{2}$, aber $A_{1}A_{2}\not \parallel B_{1}B_{2}$ (Hauptfall) oder
3. sie sind kollinear.

Kollineare Vorgaben

Bei kollinearen Vorgaben konstruiert man zunächst 2 Hilfspunkte $H_{1},H_{2}$, die nicht auf der gleichen Geraden wie die Vorgabepunkte $A_{1},A_{2},B_{1},B_{2}$ liegen.

Der 3. Fall kann durch folgende Konstruktion auf einen der anderen Fälle zurückgeführt werden:

• Wähle einen beliebigen Punkt $H_{1}$ außerhalb von $A_{1}A_{2}$.
• Zeichne die Verbindungsgeraden des Dreiecks $A_{1}H_{1}B_{1}$.
• Die Parallele zu $A_{1}H_{1}$ durch $A_{2}$ schneidet die Parallele zu $B_{1}H_{1}$ durch $B_{2}$ in einem Punkt $H_{2}$.

Damit hat man nun ein Trapez $A_{1}H_{1}H_{2}A_{2}$ und damit entweder den 1. oder den 2. Fall der obigen Fallunterscheidung (mit $H_{1},H_{2}$ an der Stelle von $B_{1},B_{2}$). Eine Dilatation $\alpha$ erfüllt die ursprünglichen Vorgaben unabhängig von der Wahl des Hilfspunktes $H_{1}$ genau dann, wenn sie $\alpha (A_{1})=A_{2};\alpha (H_{1})=H_{2}$ erfüllt.

Die Vorgaben bilden ein nichtentartetes Parallelogramm

Wenn die Vorgabepunkte ein nichtentartetes Parallelogramm bilden, dann muss die Dilatation (im Falle ihrer Existenz) eine Translation sein. Zur Konstruktion weiterer Bilder genügt eines der Punkt-Bildpunktpaare, in der hier gezeigten Konstruktion wurde $B_{1},B_{2}$ verwendet.

Im 1. Fall muss die Dilatation eine nichtidentische Translation, also fixpunktfrei sein, vergleiche die Abbildung rechts. Zu einem beliebigen Punkt $C_{1}\not \in B_{1}B_{2}$ (sonst verwende $A_{1},A_{2}$) kann der Bildpunkt so konstruiert werden: Die Parallele zu $B_{1}B_{2}$ durch $C_{1}$ schneidet die Parallele zu $B_{1}C_{1}$ durch $B_{2}$ in $C_{2}.$

Der Konstruktionstext zeigt, dass die Dilatation im Falle ihrer Existenz durch die Vorgaben eindeutig bestimmt ist. Sie existiert für den 1. Fall stets, wenn ${\mathcal {A}}$

• eine affine Translationsebene, desarguessche Ebene oder
• eine mindestens dreidimensionale affine Geometrie ist.

Es existieren auch affine Ebenen, die in keiner Richtung beliebige Parallelverschiebungen zulassen: die affinen Ausschnitte von projektiven Ebenen der Lenz-Klasse I.

Die Vorgaben bilden ein Trapez, das kein Parallelogramm ist

Im 2. Fall ist die Dilatation im Falle ihrer Existenz zentral. Vergleiche die Abbildung zum „Hauptfall“ oben in diesem Abschnitt.

• Das Zentrum $Z$ der Dilatation ist der Schnittpunkt der Geraden $A_{1}A_{2}$ mit $B_{1}B_{2}$.

Für einen beliebigen Punkt $C_{1}\not \in B_{1}B_{2}$ (sonst verwende $A_{1},A_{2}$) konstruiert man den Bildpunkt so:

• Die Parallele zu $B_{1}C_{1}$ durch $B_{2}$ schneidet die Fixgerade $ZC_{1}$ in $C_{2}.$

Aus dem Konstruktionstext folgt, dass höchstens eine Dilatation die Vorgaben erfüllen kann. Für Vorgaben, die dem Hauptfall entsprechen, existiert stets eine Dilatation, falls ${\mathcal {A}}$

• eine desarguessche Ebene ist,
• eine mindestens dreidimensionale affine Geometrie ist oder
• eine affine Translationsebene ist und das Trapez mit dem durch es bestimmten Zentrum $Z$ die Voraussetzungen des 1. Strahlensatzes für Translationsebenen erfüllt.

Literatur

Dilatation, wie in diesem Artikel definiert

• Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. In: Mathematik für das Lehramt an Gymnasien. 1. Auflage. Teubner, Stuttgart 1976, ISBN 3-519-02751-8 (Inhaltsverzeichnis [abgerufen am 14. Januar 2012]). 
• Helmut Karzel, Kay Sörensen, Dirk Windelberg: Einführung in die Geometrie. In: Studia mathematica; Uni-Taschenbücher. Taschenbuch 1. Vandenhoeck und Ruprecht, Göttingen 1973, ISBN 3-525-03406-7 (Inhaltsverzeichnis [abgerufen am 14. Januar 2012]). 
• Max Koecher, Aloys Krieg: Ebene Geometrie. 3., neu bearb. und erw. Auflage. Springer, Berlin / Heidelberg / New York 2007, ISBN 978-3-540-49327-3 (Inhaltsverzeichnis [abgerufen am 14. Januar 2012]). 

Dilatation mit anderer Bedeutung

• David Hilbert und Stephan Cohn-Vossen: Anschauliche Geometrie. 2. Auflage. Springer, Berlin / Heidelberg / New York 2011, ISBN 978-3-642-19947-9 (Inhaltsverzeichnis [abgerufen am 14. Januar 2012]). 
• Günter Scheja, Uwe Storch: Lehrbuch der Algebra: unter Einschluß der linearen Algebra. 2., überarb. und erw. Auflage. Teubner, Stuttgart 1994, ISBN 3-519-12203-0 (Inhaltsverzeichnis [abgerufen am 14. Januar 2012]). 

Weblinks

• Eric W. Weisstein: Dilation. In: MathWorld (englisch).