Benutzer:Striegistaler/Parkplatz

Transformator

Idealer Transformator

Unter einem idealen Transformator versteht man einen in der Praxis nicht realisierbaren verlustfreien Transformator. Diese Modellvorstellung ist hilfreich bei der Funktionsbeschreibung. In der Praxis treten mehr oder weniger große Abweichungen auf, die Gesetzmäßigkeiten gelten nur näherungsweise.

3D-Zeichnung eines typischen Netztransformators. Die innere Wicklung ist für Netzspannung (die Speisespannung) ausgelegt – erkennbar an der großen Windungszahl aus dünnem Draht. An der äußeren Wicklung wird die Ausgangsspannung entnommen. Sie ist meist wesentlich geringer und erfordert daher eine kleinere Windungszahl – der Strom ist jedoch höher, daher ist die Drahtdicke größer. Der Trafokern besteht aus dünnen Eisenblechen, die, um Wirbelströme zu vermeiden, gegeneinander isoliert sind.

Die exakte Beschreibung der physikalischen Vorgänge erfordert Methoden der Infinitesimalrechnung wie sie unter Elektromagnetische Induktion dargestellt sind.
Aus diesen Berechnungen folgt, dass sich beim idealen Transformator die Spannungen wie die Windungszahlen verhalten.
Sind N₁, N₂, U₁ und U₂ die Windungszahlen beziehungsweise die Effektivwerte der primär- und sekundärseitigen Spannungen, so gilt beim idealen Transformator

${\frac {U_{1}}{U_{2}}}={\frac {N_{1}}{N_{2}}}$   bzw.   $U_{2}={\frac {N_{2}}{N_{1}}}\cdot U_{1}$

Durch geeignete Wahl der Windungszahlen N₁ und N₂ können mit einem Transformator Wechselspannungen sowohl hochtransformiert werden, indem N₂ größer als N₁ gewählt wird, oder heruntertransformiert, wenn N₂ kleiner als N₁ gewählt ist.

Wird an die sekundäre Wicklung ein Verbraucher angeschlossen, so entnimmt dieser der Sekundärspule elektrische Energie, es fließt ein Strom. Auf der Sekundärseite wird die Leistung

$P_{2}=U_{2}\cdot I_{2}$

abgegeben. Genau die gleiche Leistung wird jetzt von der Primärspule dem Netz entnommen:

$P_{1}=U_{1}\cdot I_{1}$

Aus

$P_{1}=P_{2}$ folgt

$U_{1}\cdot I_{1}=U_{2}\cdot I_{2}$

Daraus ergibt sich

${\frac {U_{1}}{U_{2}}}={\frac {I_{2}}{I_{1}}}={\frac {N_{1}}{N_{2}}}$

Die Spannungen sind den Windungszahlen direkt proportional, die Ströme sind den Spannungen und den Windungszahlen umgekehrt poportional.

$I_{2}={\frac {N_{1}}{N_{2}}}\cdot I_{1}$.

Realer Transformator, Originaltext 21.03.15

Ideale Transformatoren sind praktisch nicht realisierbar. Ein realer Transformator unterscheidet sich folgendermaßen vom idealen Transformator:

• Die Wicklungen haben Widerstände und parasitäre Kapazitäten;
• im Eisenkern treten Wirbelstromverluste auf;
• die Ummagnetisierung des Kerns verbraucht Energie;
• nicht der gesamte magnetische Fluss $\Phi$, der die Primärwicklungen durchströmt, führt auch durch die Sekundärwicklungen, es treten vielmehr Streuflüsse auf;
• die Permeabilität des Kerns hängt von der Frequenz und der Stärke des Magnetflusses ab;
• die Sättigungseffekte des Kerns führen dazu, dass die Induktivität der Primärwicklungen nicht konstant ist, sondern vom primärseitigen Magnetisierungsstrom abhängt, der sich wiederum beim Durchlaufen der Magnetisierungskurve während einer Spannungshalbschwingung ändert und der beim Erreichen der totalen Eisenkernsättigung hohe Amplituden annehmen kann;
• der Kern ändert aufgrund der Magnetostriktion in geringem Maß seine Form, wenn sich das Magnetfeld ändert, was sich z. B. bei 50-Hz-Netztrafos als typisches Netzbrummen akustisch bemerkbar macht (es kann aber auch durch lockere Wicklungen oder Trafobleche verursacht werden).
• bei Leerlauf im Sekundärkreis fließt immer ein Magnetisierungsstrom im Primärkreis, der von der Größe des induktiven Blindwiderstandes der Primärtrafospule abhängt und u. U. im Primärdrahtquerschnitt mit berücksichtigt werden sollte.

Die Widerstände der Wicklungen, die Ummagnetisierung und die Wirbelströme führen zu Energieverlusten. Die Verluste aufgrund der Widerstände der Wicklungen heißen Kupferverluste, die Verluste durch die Ummagnetisierung heißen Hystereseverluste, und die Verluste aufgrund von Wirbelströmen heißen Wirbelstromverluste. Hystereseverluste und Wirbelstromverluste werden unter dem Begriff Eisenverluste zusammengefasst.

Die Kupferverluste hängen quadratisch von der Belastung des Transformators ab, d. h., sie sind proportional zum Quadrat der Ströme in jeder Wicklung I_x. Die Eisenverluste sind fast unabhängig von der Belastung, aber in etwa proportional zum Quadrat der magnetischen Flussdichte im Kern. Die Hystereseverluste sind außerdem proportional zur Frequenz, die Wirbelstromverluste sind proportional zum Quadrat der Frequenz.

Streuflüsse bewirken, dass die Sekundärspannung etwas geringer ist als beim idealen Transformator.

Die Sättigungsmagnetisierung begrenzt die mögliche Betriebsfrequenz nach unten beziehungsweise bei gegebener Frequenz und Windungszahl die mögliche Primärspannung nach oben. Wird die Grenze überschritten und die Sättigung erreicht, fließen primärseitig sehr hohe Ströme, während sekundärseitig die Spannung sehr gering wird. Durch Erhöhung der Primärwindungszahl lässt sie sich jedoch auf Kosten des Wickelraumes und der Zunahme der Kupferverluste im Praxisfall gegebenenfalls verhindern. Die Sekundärwindungszahlen erhöhen sich dann natürlich entsprechend ebenfalls. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstroms betragen.

Belasteter und unbelasteter Transformator

Wenn an die Sekundärwicklung kein Verbraucher angeschlossen ist, liegt Leerlauf vor. Der Transformator ist unbelastet. Ein verlustloser Transformator im Leerlauf verhält sich wie eine ideale Spule. Wird primärseitig eine sinusförmige Wechselspannung angeschlossen, fließt ein um 90 Grad phasenverschobener Strom, der als Magnetisierungsstrom bezeichnet wird und dem Aufbau des magnetischen Feldes dient. Beim realen Transformator ist die Phasenverschiebung des Leerlaufstroms gegenüber der Primärspannung aufgrund der Eisenverluste kleiner als 90 Grad. Im Leerlauf sind die Eisenverluste aufgrund des nur geringen Eingangsstroms viel größer als die Kupferverluste durch den Leerlaufstrom in der Primärspule.

Wegen des in der Realität meist nichtlinearen Zusammenhangs zwischen magnetischer Feldstärke $H$ und magnetischer Induktion $B$ im Kern ist der Magnetisierungsstrom, anders als beim verlustlosen Transformator, nicht sinusförmig.

Wenn der Transformator sekundärseitig belastet wird, fließt ein Sekundärstrom. Dieser ändert den Fluss im Kern und damit die in der Primärwicklung induzierte Gegenspannung. Um das Spannungsgleichgewicht auf der Primärseite aufrechtzuerhalten, muss diese Flussänderung durch einen primärseitigen Zusatzstrom zusätzlich zum Magnetisierungsstrom kompensiert werden. Es muss sich ein Gleichgewicht zwischen der vom Sekundärstrom erzeugten Durchflutung und der durch den primärseitigen Zusatzstrom bedingten Durchflutung einstellen. Bei Nennlast ist der Primärstrom deswegen viel größer als im Leerlauffall. Bei Belastung sinkt die magnetische Flussdichte geringfügig ab.

Wird die Sekundärseite kurzgeschlossen und der Eingangsstrom auf den Strom bei Nennlast geregelt, muss dazu die Primärspannung reduziert werden. Die so eingestellte Primärspannung wird als Kurzschlussspannung bezeichnet, welche nicht absolut, sondern als prozentuales Verhältnis zur Nennspannung angegeben wird. Bei Leistungstransformatoren beträgt sie zwischen 5 % und 20 %, bei Kleintransformatoren liegt sie zwischen 15 % und 40 %, bei Schweißtransformatoren beträgt sie 100 %.

Transformatoren mit hoher Kurzschlussspannung heißen spannungsweich, solche mit niedriger Kurzschlussspannung heißen spannungssteif. Die Kurzschlussspannung hängt wesentlich von der Konstruktion des Kerns und der Lage der Spulen zueinander ab: hohe Streuflüsse führen zu hohen Kurzschlussspannungen. Siehe auch Streufeldtransformator.

Als Kurzschlussstrom wird jener Strom bezeichnet, der bei sekundärseitigem Kurzschluss und Nennspannung fließt. Er ist viel höher als der Nennstrom und kann den Transformator in kurzer Zeit zerstören. Der Kurzschlussstrom ist umso höher, je niedriger die Kurzschlussspannung ist. Für Transformatoren mit niedriger Kurzschlussspannung sind Kurzschlüsse daher gefährlich. Transformatoren, die so ausgelegt sind, dass sie im Kurzschlussfall nicht zerstört werden, werden als kurzschlussfest bezeichnet. In der Regel werden nur Kleintransformatoren bis zu wenigen VA Leistung, wie zum Beispiel Klingeltrafos, kurzschlussfest ausgelegt. Aber auch große Leistungstrafos müssen zumindest einen kurzfristigen Stoßkurzschlussstrom ohne mechanische Beschädigung durch die auftretenden Lorentzkräfte überstehen können.

Wirkungsgrad

Typischer Wirkungsgradverlauf eines Transformators über die Belastung am Beispiel eines 100-VA-Netztransformators

Der Wirkungsgrad eines Transformators ist das Verhältnis der elektrischen Leistung, die den Transformator sekundärseitig verlässt, zur Leistung, die primärseitig in ihn hineinfließt. Wegen der Eisen- und Kupferverluste ist er kleiner als 1. Transformatoren hoher Nennleistung haben Wirkungsgrade von mehr als 99 %, während der Wirkungsgrad von Kleintransformatoren (z. B. 100 VA) um 80 % liegt, und Kleinsttransformatoren (1 VA) kaum auf 50 % Wirkungsgrad kommen. Bei höherer Frequenz, z. B. in Schaltnetzteilen, können auch kleine Transformatoren einen hohen Wirkungsgrad erreichen.

Kurzzeitig können Transformatoren stark überlastet werden. Vom Kurzzeit-Betrieb wird zum Beispiel bei Lötpistolen, aber auch bei Elektrolokomotiven Gebrauch gemacht. Transformatoren liefern ein Maximum an Ausgangsleistung bei einem Wirkungsgrad von 50 % (Leistungsanpassung). Im nebenstehenden Diagramm ist dieser Punkt ganz rechts am Kurvenende – der dem Beispiel zugrunde liegende Transformator liefert dort etwa das 2,5fache seiner Nennleistung.

Maschinentransformatoren sind dauernd belastet, sie werden auf maximalen Wirkungsgrad dimensioniert, d. h., dass bei Nennlast Eisen- und Kupferverluste etwa gleich hoch sind.
Bei einem Ortsnetztransformator, der im Stromnetz verwendet wird, liegt die mittlere Belastungsdauer nur bei ungefähr 40 % der Einschaltdauer, daher können hier höhere Kupferverluste in Kauf genommen werden, während die Eisenverluste stärker reduziert werden. Solche Transformatoren werden hinsichtlich ihres Jahreswirkungsgrades optimiert. Damit wird das Verhältnis der insgesamt pro Jahr primär- und sekundärseitig umgesetzten Energiemengen bezeichnet. Der Jahreswirkungsgrad liegt umso höher, je größer das Verhältnis zwischen Belastungs- und Einschaltdauer ist.

Netzwerkmodellierung

Ersatzschaltbild eines realen Transformators

Die Netzwerkmodellierung eines Transformators verfolgt das Ziel, die wesentlichen nichtidealen Eigenschaften eines Transformators mit einer geringen Zahl an Parametern zu beschreiben. Das nebenstehende Ersatzschaltbild zeigt eine häufig vorgenommene Modellierung mithilfe von linearen Bauelementen. Dabei haben die einzelnen Bauelemente die folgende Bedeutung:

• $U_{p}$: primärseitige Spannungsquelle
• $U_{s}=U_{2}$: Ausgangsspannung
• $I_{1}$, $I_{2}'$: Eingangsstrom und transformierter Ausgangsstrom
• $R_{q1}$: Innenwiderstand der primärseitigen Spannungsquelle
• $L_{\sigma 1}$, $L'_{\sigma 2}$: Streuinduktivität der Primärseite und transformierte Streuinduktivität der Sekundärseite
• $R_{1}$, $R'_{2}$: Wicklungswiderstand der Primärseite und transformierter Wicklungswiderstand der Sekundärseite
• $L_{h1}$: Hauptinduktivität, die den Magnetisierungsstrom führt
• $R_{Fe}$: lineare Modellierung der meist nichtlinearen Eisenverluste im Kern (Fe: Eisen)

Auf die Modellierung der parasitären Kapazitäten der Wicklungen wurde im abgebildeten Modell verzichtet. Ebenso werden nichtlineare Eigenschaften des Transformators nicht abgebildet.

Der eingezeichnete ideale Transformator gehorcht den Transformationsgleichungen:

${\frac {{\underline {U}}_{1}}{{\underline {U}}_{2}}}=\gamma {\text{ und }}{\frac {{\underline {I}}_{1}}{{\underline {I}}_{2}}}={\frac {1}{\gamma }}.$

Der Übertragungsfaktor $\gamma =N_{1}/N_{2}$ bezeichnet dabei das Verhältnis der Windungszahlen von Primär- und Sekundärseite.

Die Größen, die mit einem zusätzlichen Strich ' gekennzeichnet sind, wurden von der Sekundärseite zur Primärseite transformiert. Bei der Transformation einer Impedanz ${\underline {Z}}$ von der Sekundärseite zu einer Impedanz $Z'$ auf der Primärseite gilt die folgende Transformationsgleichung:

${\underline {Z'}}=\gamma ^{2}{\underline {Z}}$

Die Impedanztransformation bedeutet, dass die Eingangsklemmen eines Transformators für einen elektrischen Schaltkreis wie ein Widerstand $\gamma ^{2}\cdot R$ wirken, wenn an die Sekundärseite ein Widerstand R angeschlossen wird. Somit können mithilfe eines Transformators Widerstände vergrößert oder verkleinert werden, indem das Windungsverhältnis $\gamma$ geändert wird.

Die Impedanztransformation wird in elektronischen Schaltungen häufig zur Anpassung eines Netzwerkes an den Wellenwiderstand einer Leitung oder zur Leistungsanpassung eingesetzt. Anders als bei gyratorischer Kopplung bleibt bei transformatorischer Kopplung die Struktur des Netzwerkes erhalten, das heißt Reihen- und Parallelschaltungen bleiben erhalten, und induktives und kapazitives Verhalten werden nicht gegeneinander ausgetauscht.

Wenn es auf die galvanische Trennung des Transformators nicht ankommt, kann der ideale Transformator im Ersatzschaltbild nach Transformation aller sekundärseitigen Bauelemente auf die Primärseite entfallen.

Signalformen und Bandbreite

Die Speisung mit einer sinusförmigen Eingangsspannung ist typisch für Leistungstransformatoren, wie sie beispielsweise im öffentlichen Stromnetz eingesetzt werden. Die Netzfrequenz in einem Stromnetz ist durch die Umdrehungsgeschwindigkeit der Generatoren vorgegeben. Typische Werte für die Netzfrequenz sind 50 Hz (öffentliches Stromnetz in Europa) und 60 Hz (Stromnetz in den USA). In der Bahnstromversorgung gibt es darüber hinaus auch Netze mit Netzfrequenzen von 16,7 Hz und 25 Hz.

In PC-Netzteilen, Frequenzumrichtern und den Wechselrichtern der Photovoltaik werden in speziellen Schaltnetzteilen Rechteckspannungen mit wesentlich höheren Frequenzen erzeugt und transformiert. Die dabei eingesetzten Transformatoren dienen vorwiegend zur galvanischen Trennung und zur Spannungsanpassung, wobei eine Sättigung des Transformatorkerns vermieden wird.

In Sperrwandlern werden zwei magnetisch gekoppelte Spulen mit einem Kern mit Luftspalt als Energiespeicher verwendet. Die über die Primärseite ins magnetische Feld eingebrachte Energie wird nicht sofort entnommen, sondern erst nach Abschalten der Eingangsspannung an der Sekundärseite abgegriffen. Bei rechteckförmigen Eingangsspannungen ergeben sich somit annähernd dreieckförmige Eingangsströme.

Bei der Übertragung von Signalen mit einem Transformator ist es wichtig, dass die Signalanteile aller relevanten Frequenzen übertragen werden. Bei Verwendung einer ohmschen Last weist der Transformator ein sogenanntes Bandpassverhalten auf. Bei ungeeigneter Dimensionierung oder falscher Beschaltung kann ein Transformator darüber hinaus ein unerwünschtes Schwingverhalten, eine sogenannte Resonanzüberhöhung, aufweisen.

Die Begrenzung der Bandbreite nach unten kommt durch die Hauptinduktivität $L_{h1}$ zustande. Sie schließt Signale niedriger Frequenzen kurz. Nach oben erfolgt die Begrenzung der Bandbreite im Netzwerkmodell allein durch die Streuinduktivitäten $L_{\sigma 1}$ und $L_{\sigma 2}$. Ihre Impedanz steigt mit der Frequenz und verhindert auf diese Weise eine Signalübertragung. Bei hohen Frequenzen ist außerdem die kapazitive Kopplung zwischen den einzelnen Windungen relevant.

In der Praxis ist der Frequenzbereich von Transformatoren nach unten vorwiegend durch die erforderliche Größe begrenzt, die mit sinkender Frequenz stark ansteigt. Der typische Frequenzbereich von Niederfrequenztransformatoren reicht bis 16,7 Hz hinunter, der Nennfrequenz für die Bahnstromversorgung. Am oberen Ende des Frequenzbereiches stehen Transformatoren der Hochfrequenztechnik, bei denen die Wicklungen häufig nur noch aus wenigen oder sogar nur einer einzigen Windung bestehen. Die Frequenzspanne handelsüblicher Hochfrequenztransformatoren umfasst einen Bereich von wenigen MHz bis etwa 1 GHz.

Verhalten bei Netzstörungen und beim Einschalten

Verlauf von Strom und Spannung bei Netzstörungen am belasteten Transformator

Typisches Verhalten eines Transformators beim Einschalten. Das Maximum des Magnetisierungsstroms liegt nach der ersten Spannungshalbwelle.

Einschaltvorgänge und Netzstörungen bewirken besonders starke Abweichungen des Transformatorverhaltens vom idealen Verhalten. Beide Vorgänge können den Transformatorkern sättigen und zu beträchtlichen Überströmen führen.

Entsprechend dem Induktionsgesetz entscheidet allein der Verlauf der Eingangsspannung, ob bei einem Transformator Sättigungserscheinungen auftreten oder nicht. Der Belastungszustand spielt keine wesentliche Rolle; selbst ein Kurzschluss auf der Sekundärseite führt nicht zur Sättigung.

Bei einer typischen Netzstörung im 230-V-Netz fallen vereinfacht betrachtet einzelne oder mehrere Spannungshalbwellen beziehungsweise Teile davon aus. Der Transformator reagiert auf das Ausfallen der Netzhalbwelle mit einem großen Sättigungsstrom in der darauf folgenden Halbwelle. Den wesentlichen Beitrag zur Kernsättigung liefert die Vormagnetisierung des Kerns, die durch die Störung der Eingangsspannung verursacht wird.

Beim Abschalten oder Ausfall der Spannung verharrt der Magnetisierungszustand des Kerns in dem Remanenzpunkt, der der Magnetisierung im Abschaltzeitpunkt am nächsten liegt. Abhängig von Polarität und Phasenlage der wiederkehrenden Netzspannung kann das dazu führen, dass ausgehend von diesem Remanenzpunkt der verbleibende Induktionshub bis zur beginnenden Sättigung kleiner ist als die Zeitfläche der wiederkehrenden Spannungshalbwelle. Die durch die Zeitfläche der wiederkehrenden Halbwelle erzwungene Flussänderung im Kern treibt diesen in die Sättigung, wobei große Magnetisierungsströme benötigt werden.

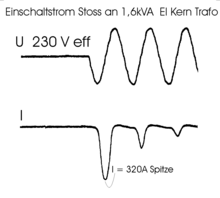
Der ungünstigste Fall für einen Luftkern ist das Einschalten einer vollen Halbwelle, was zum 2-fachen Magnetisierungsstrom des Nennwertes führt. Der ungünstigste Fall für einen Ringkern ist das Einschalten, wenn die Remanenz bei $B=B_{\mathrm {max} }$ liegt und die Polarität der wiederkehrenden Spannung identisch ist mit der vor dem Abschalten. Diesen Verlauf zeigt die untere Prinzipskizze. Der Magnetisierungsstrom ist in diesem Fall im Wesentlichen nur noch durch die Restinduktivität und durch den ohmschen Widerstand der Primärspule und die Impedanz der Netzzuleitung begrenzt. Er kann demnach extreme Werte annehmen, weil der Transformatorkern restlos gesättigt ist und keine Magnetflussänderung mehr aufnehmen kann. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstromes betragen.

Diese Einschaltvorgänge klingen in jedem Fall im Verlauf einiger Halbwellen ab, da aufgrund der Asymmetrie der Magnetisierungsströme auch die beiden gegenpoligen Spannungshalbwellen mit unsymmetrischen Spannungsabfällen behaftet sind. Das hat zur Folge, dass in der Sättigungshalbwelle stets etwas weniger Spannung zur Aufmagnetisierung zur Verfügung steht als bei der dazu gegenpoligen Spannungshalbwelle die zur Abmagnetisierung führt. Dadurch zentriert sich der Magnetisierungs-Schleifendurchlauf selbsttätig nach einigen Netzperioden, wobei die Zeitkonstante dafür aus dem Quotienten der Induktivität dividiert durch die Ohmschen Widerstände im Stromkreis errechnet werden kann. Bei sehr großen Transformatoren kann diese Zeitkonstante deshalb einige Minuten betragen.

Schlienz gibt als Zahlenwert für einen daraufhin optimierten 1,6-kVA-Transformator (230 V), der mit 1 kW belastet wird, einen Strom von 200 A aufgrund der Sättigung an. Im Vergleich dazu fließen im Normalbetrieb weniger als 10 A.

Realer Transformator, Bearbeitung ab 21.03.15

Im Unterschied zum Denkmodell Idealer Transformator müssen bei der praktischen Realisierung eines Transformators Eigenschaften der verwendeten Materialien und physikalische Effekte berücksichtigt werden. Das führt dazu, dass die für den idealen Transformator gefundenen Gesetze nur näherungsweise gelten. Durch die Widerstände der Wicklungen, die Ummagnetisierung und die Wirbelströme im Eisenkern wird ein Teil der elektrischen Energie in Wärmeenergie umgewandelt. Dadurch ist der Wirkungsgrad eines realen Transformators kleiner 100%. Die Verluste aufgrund der Widerstände der Wicklungen heißen Kupferverluste, die Verluste durch die Ummagnetisierung heißen Hystereseverluste, und die Verluste aufgrund von Wirbelströmen heißen Wirbelstromverluste. Hystereseverluste und Wirbelstromverluste werden unter dem Begriff Eisenverluste zusammengefasst.

Verluste, Materialeigenschaften nur summarisch nennen, Details in Extrapunkt auslagern hier versteckt

auf Ferromagnetismus Grafik B=f(H) - für später!
Zeigermodell

Belasteter und unbelasteter realer Transformator

muss noch ausgemistet werden, zur späteren Verwendung zunächst verstecken
evtl. aufteilen: Unbelasteter realer Transformato, Belasteter realer Transformator

Wenn an die Sekundärwicklung kein Verbraucher angeschlossen ist, liegt Leerlauf vor. Der Transformator ist unbelastet. Ein verlustloser Transformator im Leerlauf verhält sich wie eine ideale Spule. Wird primärseitig eine sinusförmige Wechselspannung angeschlossen, fließt ein um 90 Grad phasenverschobener Strom, der als Magnetisierungsstrom bezeichnet wird und dem Aufbau des magnetischen Feldes dient. Beim realen Transformator ist die Phasenverschiebung des Leerlaufstroms gegenüber der Primärspannung aufgrund der Eisenverluste kleiner als 90 Grad. Im Leerlauf sind die Eisenverluste aufgrund des nur geringen Eingangsstroms viel größer als die Kupferverluste durch den Leerlaufstrom in der Primärspule.

Wegen des in der Realität meist nichtlinearen Zusammenhangs zwischen magnetischer Feldstärke $H$ und magnetischer Induktion $B$ im Kern ist der Magnetisierungsstrom, anders als beim verlustlosen Transformator, nicht sinusförmig.

Wenn der Transformator sekundärseitig belastet wird, fließt ein Sekundärstrom. Dieser ändert den Fluss im Kern und damit die in der Primärwicklung induzierte Gegenspannung. Um das Spannungsgleichgewicht auf der Primärseite aufrechtzuerhalten, muss diese Flussänderung durch einen primärseitigen Zusatzstrom zusätzlich zum Magnetisierungsstrom kompensiert werden. Es muss sich ein Gleichgewicht zwischen der vom Sekundärstrom erzeugten Durchflutung und der durch den primärseitigen Zusatzstrom bedingten Durchflutung einstellen. Bei Nennlast ist der Primärstrom deswegen viel größer als im Leerlauffall. Bei Belastung sinkt die magnetische Flussdichte geringfügig ab.

Wird die Sekundärseite kurzgeschlossen und der Eingangsstrom auf den Strom bei Nennlast geregelt, muss dazu die Primärspannung reduziert werden. Die so eingestellte Primärspannung wird als Kurzschlussspannung bezeichnet, welche nicht absolut, sondern als prozentuales Verhältnis zur Nennspannung angegeben wird. Bei Leistungstransformatoren beträgt sie zwischen 5 % und 20 %, bei Kleintransformatoren liegt sie zwischen 15 % und 40 %, bei Schweißtransformatoren beträgt sie 100 %.

Transformatoren mit hoher Kurzschlussspannung heißen spannungsweich, solche mit niedriger Kurzschlussspannung heißen spannungssteif. Die Kurzschlussspannung hängt wesentlich von der Konstruktion des Kerns und der Lage der Spulen zueinander ab: hohe Streuflüsse führen zu hohen Kurzschlussspannungen. Siehe auch Streufeldtransformator.

Als Kurzschlussstrom wird jener Strom bezeichnet, der bei sekundärseitigem Kurzschluss und Nennspannung fließt. Er ist viel höher als der Nennstrom und kann den Transformator in kurzer Zeit zerstören. Der Kurzschlussstrom ist umso höher, je niedriger die Kurzschlussspannung ist. Für Transformatoren mit niedriger Kurzschlussspannung sind Kurzschlüsse daher gefährlich. Transformatoren, die so ausgelegt sind, dass sie im Kurzschlussfall nicht zerstört werden, werden als kurzschlussfest bezeichnet. In der Regel werden nur Kleintransformatoren bis zu wenigen VA Leistung, wie zum Beispiel Klingeltrafos, kurzschlussfest ausgelegt. Aber auch große Leistungstrafos müssen zumindest einen kurzfristigen Stoßkurzschlussstrom ohne mechanische Beschädigung durch die auftretenden Lorentzkräfte überstehen können.

Wirkungsgrad

Typischer Wirkungsgradverlauf eines Transformators über die Belastung am Beispiel eines 100-VA-Netztransformators

Der Wirkungsgrad eines Transformators ist das Verhältnis der elektrischen Leistung, die den Transformator sekundärseitig verlässt, zur Leistung, die primärseitig in ihn hineinfließt. Wegen der Eisen- und Kupferverluste ist er kleiner als 1. Transformatoren hoher Nennleistung haben Wirkungsgrade von mehr als 99 %, während der Wirkungsgrad von Kleintransformatoren (z. B. 100 VA) um 80 % liegt, und Kleinsttransformatoren (1 VA) kaum auf 50 % Wirkungsgrad kommen. Bei höherer Frequenz, z. B. in Schaltnetzteilen, können auch kleine Transformatoren einen hohen Wirkungsgrad erreichen.

Kurzzeitig können Transformatoren stark überlastet werden. Vom Kurzzeit-Betrieb wird zum Beispiel bei Lötpistolen, aber auch bei Elektrolokomotiven Gebrauch gemacht. Transformatoren liefern ein Maximum an Ausgangsleistung bei einem Wirkungsgrad von 50 % (Leistungsanpassung). Im nebenstehenden Diagramm ist dieser Punkt ganz rechts am Kurvenende – der dem Beispiel zugrunde liegende Transformator liefert dort etwa das 2,5fache seiner Nennleistung.

Maschinentransformatoren sind dauernd belastet, sie werden auf maximalen Wirkungsgrad dimensioniert, d. h., dass bei Nennlast Eisen- und Kupferverluste etwa gleich hoch sind.
Bei einem Ortsnetztransformator, der im Stromnetz verwendet wird, liegt die mittlere Belastungsdauer nur bei ungefähr 40 % der Einschaltdauer, daher können hier höhere Kupferverluste in Kauf genommen werden, während die Eisenverluste stärker reduziert werden. Solche Transformatoren werden hinsichtlich ihres Jahreswirkungsgrades optimiert. Damit wird das Verhältnis der insgesamt pro Jahr primär- und sekundärseitig umgesetzten Energiemengen bezeichnet. Der Jahreswirkungsgrad liegt umso höher, je größer das Verhältnis zwischen Belastungs- und Einschaltdauer ist.

Netzwerkmodellierung

Ersatzschaltbild eines realen Transformators

Die Netzwerkmodellierung eines Transformators verfolgt das Ziel, die wesentlichen nichtidealen Eigenschaften eines Transformators mit einer geringen Zahl an Parametern zu beschreiben. Das nebenstehende Ersatzschaltbild zeigt eine häufig vorgenommene Modellierung mithilfe von linearen Bauelementen. Dabei haben die einzelnen Bauelemente die folgende Bedeutung:

• $U_{p}$: primärseitige Spannungsquelle
• $U_{s}=U_{2}$: Ausgangsspannung
• $I_{1}$, $I_{2}'$: Eingangsstrom und transformierter Ausgangsstrom
• $R_{q1}$: Innenwiderstand der primärseitigen Spannungsquelle
• $L_{\sigma 1}$, $L'_{\sigma 2}$: Streuinduktivität der Primärseite und transformierte Streuinduktivität der Sekundärseite
• $R_{1}$, $R'_{2}$: Wicklungswiderstand der Primärseite und transformierter Wicklungswiderstand der Sekundärseite
• $L_{h1}$: Hauptinduktivität, die den Magnetisierungsstrom führt
• $R_{Fe}$: lineare Modellierung der meist nichtlinearen Eisenverluste im Kern (Fe: Eisen)

Auf die Modellierung der parasitären Kapazitäten der Wicklungen wurde im abgebildeten Modell verzichtet. Ebenso werden nichtlineare Eigenschaften des Transformators nicht abgebildet.

Der eingezeichnete ideale Transformator gehorcht den Transformationsgleichungen:

${\frac {{\underline {U}}_{1}}{{\underline {U}}_{2}}}=\gamma {\text{ und }}{\frac {{\underline {I}}_{1}}{{\underline {I}}_{2}}}={\frac {1}{\gamma }}.$

Der Übertragungsfaktor $\gamma =N_{1}/N_{2}$ bezeichnet dabei das Verhältnis der Windungszahlen von Primär- und Sekundärseite.

Die Größen, die mit einem zusätzlichen Strich ' gekennzeichnet sind, wurden von der Sekundärseite zur Primärseite transformiert. Bei der Transformation einer Impedanz ${\underline {Z}}$ von der Sekundärseite zu einer Impedanz $Z'$ auf der Primärseite gilt die folgende Transformationsgleichung:

${\underline {Z'}}=\gamma ^{2}{\underline {Z}}$

Die Impedanztransformation bedeutet, dass die Eingangsklemmen eines Transformators für einen elektrischen Schaltkreis wie ein Widerstand $\gamma ^{2}\cdot R$ wirken, wenn an die Sekundärseite ein Widerstand R angeschlossen wird. Somit können mithilfe eines Transformators Widerstände vergrößert oder verkleinert werden, indem das Windungsverhältnis $\gamma$ geändert wird.

Die Impedanztransformation wird in elektronischen Schaltungen häufig zur Anpassung eines Netzwerkes an den Wellenwiderstand einer Leitung oder zur Leistungsanpassung eingesetzt. Anders als bei gyratorischer Kopplung bleibt bei transformatorischer Kopplung die Struktur des Netzwerkes erhalten, das heißt Reihen- und Parallelschaltungen bleiben erhalten, und induktives und kapazitives Verhalten werden nicht gegeneinander ausgetauscht.

Wenn es auf die galvanische Trennung des Transformators nicht ankommt, kann der ideale Transformator im Ersatzschaltbild nach Transformation aller sekundärseitigen Bauelemente auf die Primärseite entfallen.

Signalformen und Bandbreite

Die Speisung mit einer sinusförmigen Eingangsspannung ist typisch für Leistungstransformatoren, wie sie beispielsweise im öffentlichen Stromnetz eingesetzt werden. Die Netzfrequenz in einem Stromnetz ist durch die Umdrehungsgeschwindigkeit der Generatoren vorgegeben. Typische Werte für die Netzfrequenz sind 50 Hz (öffentliches Stromnetz in Europa) und 60 Hz (Stromnetz in den USA). In der Bahnstromversorgung gibt es darüber hinaus auch Netze mit Netzfrequenzen von 16,7 Hz und 25 Hz.

In PC-Netzteilen, Frequenzumrichtern und den Wechselrichtern der Photovoltaik werden in speziellen Schaltnetzteilen Rechteckspannungen mit wesentlich höheren Frequenzen erzeugt und transformiert. Die dabei eingesetzten Transformatoren dienen vorwiegend zur galvanischen Trennung und zur Spannungsanpassung, wobei eine Sättigung des Transformatorkerns vermieden wird.

In Sperrwandlern werden zwei magnetisch gekoppelte Spulen mit einem Kern mit Luftspalt als Energiespeicher verwendet. Die über die Primärseite ins magnetische Feld eingebrachte Energie wird nicht sofort entnommen, sondern erst nach Abschalten der Eingangsspannung an der Sekundärseite abgegriffen. Bei rechteckförmigen Eingangsspannungen ergeben sich somit annähernd dreieckförmige Eingangsströme.

Bei der Übertragung von Signalen mit einem Transformator ist es wichtig, dass die Signalanteile aller relevanten Frequenzen übertragen werden. Bei Verwendung einer ohmschen Last weist der Transformator ein sogenanntes Bandpassverhalten auf. Bei ungeeigneter Dimensionierung oder falscher Beschaltung kann ein Transformator darüber hinaus ein unerwünschtes Schwingverhalten, eine sogenannte Resonanzüberhöhung, aufweisen.

Die Begrenzung der Bandbreite nach unten kommt durch die Hauptinduktivität $L_{h1}$ zustande. Sie schließt Signale niedriger Frequenzen kurz. Nach oben erfolgt die Begrenzung der Bandbreite im Netzwerkmodell allein durch die Streuinduktivitäten $L_{\sigma 1}$ und $L_{\sigma 2}$. Ihre Impedanz steigt mit der Frequenz und verhindert auf diese Weise eine Signalübertragung. Bei hohen Frequenzen ist außerdem die kapazitive Kopplung zwischen den einzelnen Windungen relevant.

In der Praxis ist der Frequenzbereich von Transformatoren nach unten vorwiegend durch die erforderliche Größe begrenzt, die mit sinkender Frequenz stark ansteigt. Der typische Frequenzbereich von Niederfrequenztransformatoren reicht bis 16,7 Hz hinunter, der Nennfrequenz für die Bahnstromversorgung. Am oberen Ende des Frequenzbereiches stehen Transformatoren der Hochfrequenztechnik, bei denen die Wicklungen häufig nur noch aus wenigen oder sogar nur einer einzigen Windung bestehen. Die Frequenzspanne handelsüblicher Hochfrequenztransformatoren umfasst einen Bereich von wenigen MHz bis etwa 1 GHz.

Verhalten bei Netzstörungen und beim Einschalten

Verlauf von Strom und Spannung bei Netzstörungen am belasteten Transformator

Typisches Verhalten eines Transformators beim Einschalten. Das Maximum des Magnetisierungsstroms liegt nach der ersten Spannungshalbwelle.

Einschaltvorgänge und Netzstörungen bewirken besonders starke Abweichungen des Transformatorverhaltens vom idealen Verhalten. Beide Vorgänge können den Transformatorkern sättigen und zu beträchtlichen Überströmen führen.

Entsprechend dem Induktionsgesetz entscheidet allein der Verlauf der Eingangsspannung, ob bei einem Transformator Sättigungserscheinungen auftreten oder nicht. Der Belastungszustand spielt keine wesentliche Rolle; selbst ein Kurzschluss auf der Sekundärseite führt nicht zur Sättigung.

Bei einer typischen Netzstörung im 230-V-Netz fallen vereinfacht betrachtet einzelne oder mehrere Spannungshalbwellen beziehungsweise Teile davon aus. Der Transformator reagiert auf das Ausfallen der Netzhalbwelle mit einem großen Sättigungsstrom in der darauf folgenden Halbwelle. Den wesentlichen Beitrag zur Kernsättigung liefert die Vormagnetisierung des Kerns, die durch die Störung der Eingangsspannung verursacht wird.

Beim Abschalten oder Ausfall der Spannung verharrt der Magnetisierungszustand des Kerns in dem Remanenzpunkt, der der Magnetisierung im Abschaltzeitpunkt am nächsten liegt. Abhängig von Polarität und Phasenlage der wiederkehrenden Netzspannung kann das dazu führen, dass ausgehend von diesem Remanenzpunkt der verbleibende Induktionshub bis zur beginnenden Sättigung kleiner ist als die Zeitfläche der wiederkehrenden Spannungshalbwelle. Die durch die Zeitfläche der wiederkehrenden Halbwelle erzwungene Flussänderung im Kern treibt diesen in die Sättigung, wobei große Magnetisierungsströme benötigt werden.

Der ungünstigste Fall für einen Luftkern ist das Einschalten einer vollen Halbwelle, was zum 2-fachen Magnetisierungsstrom des Nennwertes führt. Der ungünstigste Fall für einen Ringkern ist das Einschalten, wenn die Remanenz bei $B=B_{\mathrm {max} }$ liegt und die Polarität der wiederkehrenden Spannung identisch ist mit der vor dem Abschalten. Diesen Verlauf zeigt die untere Prinzipskizze. Der Magnetisierungsstrom ist in diesem Fall im Wesentlichen nur noch durch die Restinduktivität und durch den ohmschen Widerstand der Primärspule und die Impedanz der Netzzuleitung begrenzt. Er kann demnach extreme Werte annehmen, weil der Transformatorkern restlos gesättigt ist und keine Magnetflussänderung mehr aufnehmen kann. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstromes betragen.

Diese Einschaltvorgänge klingen in jedem Fall im Verlauf einiger Halbwellen ab, da aufgrund der Asymmetrie der Magnetisierungsströme auch die beiden gegenpoligen Spannungshalbwellen mit unsymmetrischen Spannungsabfällen behaftet sind. Das hat zur Folge, dass in der Sättigungshalbwelle stets etwas weniger Spannung zur Aufmagnetisierung zur Verfügung steht als bei der dazu gegenpoligen Spannungshalbwelle die zur Abmagnetisierung führt. Dadurch zentriert sich der Magnetisierungs-Schleifendurchlauf selbsttätig nach einigen Netzperioden, wobei die Zeitkonstante dafür aus dem Quotienten der Induktivität dividiert durch die Ohmschen Widerstände im Stromkreis errechnet werden kann. Bei sehr großen Transformatoren kann diese Zeitkonstante deshalb einige Minuten betragen.

Schlienz gibt als Zahlenwert für einen daraufhin optimierten 1,6-kVA-Transformator (230 V), der mit 1 kW belastet wird, einen Strom von 200 A aufgrund der Sättigung an. Im Vergleich dazu fließen im Normalbetrieb weniger als 10 A.

Realer Transformator

Ideale Transformatoren sind praktisch nicht realisierbar. Ein realer Transformator unterscheidet sich folgendermaßen vom idealen Transformator:

• Die Wicklungen haben Widerstände und parasitäre Kapazitäten;
• im Eisenkern treten Wirbelstromverluste auf;
• die Ummagnetisierung des Kerns verbraucht Energie;
• nicht der gesamte magnetische Fluss $\Phi$, der die Primärwicklungen durchströmt, führt auch durch die Sekundärwicklungen, es treten vielmehr Streuflüsse auf;
• die Permeabilität des Kerns hängt von der Frequenz und der Stärke des Magnetflusses ab;
• die Sättigungseffekte des Kerns führen dazu, dass die Induktivität der Primärwicklungen nicht konstant ist, sondern vom primärseitigen Magnetisierungsstrom abhängt, der sich wiederum beim Durchlaufen der Magnetisierungskurve während einer Spannungshalbschwingung ändert und der beim Erreichen der totalen Eisenkernsättigung hohe Amplituden annehmen kann;
• der Kern ändert aufgrund der Magnetostriktion in geringem Maß seine Form, wenn sich das Magnetfeld ändert, was sich z. B. bei 50-Hz-Netztrafos als typisches Netzbrummen akustisch bemerkbar macht (es kann aber auch durch lockere Wicklungen oder Trafobleche verursacht werden).
• bei Leerlauf im Sekundärkreis fließt immer ein Magnetisierungsstrom im Primärkreis, der von der Größe des induktiven Blindwiderstandes der Primärtrafospule abhängt und u. U. im Primärdrahtquerschnitt mit berücksichtigt werden sollte.

Die Widerstände der Wicklungen, die Ummagnetisierung und die Wirbelströme führen zu Energieverlusten. Die Verluste aufgrund der Widerstände der Wicklungen heißen Kupferverluste, die Verluste durch die Ummagnetisierung heißen Hystereseverluste, und die Verluste aufgrund von Wirbelströmen heißen Wirbelstromverluste. Hystereseverluste und Wirbelstromverluste werden unter dem Begriff Eisenverluste zusammengefasst.

Die Kupferverluste hängen quadratisch von der Belastung des Transformators ab, d. h., sie sind proportional zum Quadrat der Ströme in jeder Wicklung I_x. Die Eisenverluste sind fast unabhängig von der Belastung, aber in etwa proportional zum Quadrat der magnetischen Flussdichte im Kern. Die Hystereseverluste sind außerdem proportional zur Frequenz, die Wirbelstromverluste sind proportional zum Quadrat der Frequenz.

Streuflüsse bewirken, dass die Sekundärspannung etwas geringer ist als beim idealen Transformator.

Die Sättigungsmagnetisierung begrenzt die mögliche Betriebsfrequenz nach unten beziehungsweise bei gegebener Frequenz und Windungszahl die mögliche Primärspannung nach oben. Wird die Grenze überschritten und die Sättigung erreicht, fließen primärseitig sehr hohe Ströme, während sekundärseitig die Spannung sehr gering wird. Durch Erhöhung der Primärwindungszahl lässt sie sich jedoch auf Kosten des Wickelraumes und der Zunahme der Kupferverluste im Praxisfall gegebenenfalls verhindern. Die Sekundärwindungszahlen erhöhen sich dann natürlich entsprechend ebenfalls. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstroms betragen.

Belasteter und unbelasteter Transformator

Wenn an die Sekundärwicklung kein Verbraucher angeschlossen ist, liegt Leerlauf vor. Der Transformator ist unbelastet. Ein verlustloser Transformator im Leerlauf verhält sich wie eine ideale Spule. Wird primärseitig eine sinusförmige Wechselspannung angeschlossen, fließt ein um 90 Grad phasenverschobener Strom, der als Magnetisierungsstrom bezeichnet wird und dem Aufbau des magnetischen Feldes dient. Beim realen Transformator ist die Phasenverschiebung des Leerlaufstroms gegenüber der Primärspannung aufgrund der Eisenverluste kleiner als 90 Grad. Im Leerlauf sind die Eisenverluste aufgrund des nur geringen Eingangsstroms viel größer als die Kupferverluste durch den Leerlaufstrom in der Primärspule.

Wegen des in der Realität meist nichtlinearen Zusammenhangs zwischen magnetischer Feldstärke $H$ und magnetischer Induktion $B$ im Kern ist der Magnetisierungsstrom, anders als beim verlustlosen Transformator, nicht sinusförmig.

Wenn der Transformator sekundärseitig belastet wird, fließt ein Sekundärstrom. Dieser ändert den Fluss im Kern und damit die in der Primärwicklung induzierte Gegenspannung. Um das Spannungsgleichgewicht auf der Primärseite aufrechtzuerhalten, muss diese Flussänderung durch einen primärseitigen Zusatzstrom zusätzlich zum Magnetisierungsstrom kompensiert werden. Es muss sich ein Gleichgewicht zwischen der vom Sekundärstrom erzeugten Durchflutung und der durch den primärseitigen Zusatzstrom bedingten Durchflutung einstellen. Bei Nennlast ist der Primärstrom deswegen viel größer als im Leerlauffall. Bei Belastung sinkt die magnetische Flussdichte geringfügig ab.

Wird die Sekundärseite kurzgeschlossen und der Eingangsstrom auf den Strom bei Nennlast geregelt, muss dazu die Primärspannung reduziert werden. Die so eingestellte Primärspannung wird als Kurzschlussspannung bezeichnet, welche nicht absolut, sondern als prozentuales Verhältnis zur Nennspannung angegeben wird. Bei Leistungstransformatoren beträgt sie zwischen 5 % und 20 %, bei Kleintransformatoren liegt sie zwischen 15 % und 40 %, bei Schweißtransformatoren beträgt sie 100 %.

Transformatoren mit hoher Kurzschlussspannung heißen spannungsweich, solche mit niedriger Kurzschlussspannung heißen spannungssteif. Die Kurzschlussspannung hängt wesentlich von der Konstruktion des Kerns und der Lage der Spulen zueinander ab: hohe Streuflüsse führen zu hohen Kurzschlussspannungen. Siehe auch Streufeldtransformator.

Als Kurzschlussstrom wird jener Strom bezeichnet, der bei sekundärseitigem Kurzschluss und Nennspannung fließt. Er ist viel höher als der Nennstrom und kann den Transformator in kurzer Zeit zerstören. Der Kurzschlussstrom ist umso höher, je niedriger die Kurzschlussspannung ist. Für Transformatoren mit niedriger Kurzschlussspannung sind Kurzschlüsse daher gefährlich. Transformatoren, die so ausgelegt sind, dass sie im Kurzschlussfall nicht zerstört werden, werden als kurzschlussfest bezeichnet. In der Regel werden nur Kleintransformatoren bis zu wenigen VA Leistung, wie zum Beispiel Klingeltrafos, kurzschlussfest ausgelegt. Aber auch große Leistungstrafos müssen zumindest einen kurzfristigen Stoßkurzschlussstrom ohne mechanische Beschädigung durch die auftretenden Lorentzkräfte überstehen können.

Wirkungsgrad

Typischer Wirkungsgradverlauf eines Transformators über die Belastung am Beispiel eines 100-VA-Netztransformators

Der Wirkungsgrad eines Transformators ist das Verhältnis der elektrischen Leistung, die den Transformator sekundärseitig verlässt, zur Leistung, die primärseitig in ihn hineinfließt. Wegen der Eisen- und Kupferverluste ist er kleiner als 1. Transformatoren hoher Nennleistung haben Wirkungsgrade von mehr als 99 %, während der Wirkungsgrad von Kleintransformatoren (z. B. 100 VA) um 80 % liegt, und Kleinsttransformatoren (1 VA) kaum auf 50 % Wirkungsgrad kommen. Bei höherer Frequenz, z. B. in Schaltnetzteilen, können auch kleine Transformatoren einen hohen Wirkungsgrad erreichen.

Kurzzeitig können Transformatoren stark überlastet werden. Vom Kurzzeit-Betrieb wird zum Beispiel bei Lötpistolen, aber auch bei Elektrolokomotiven Gebrauch gemacht. Transformatoren liefern ein Maximum an Ausgangsleistung bei einem Wirkungsgrad von 50 % (Leistungsanpassung). Im nebenstehenden Diagramm ist dieser Punkt ganz rechts am Kurvenende – der dem Beispiel zugrunde liegende Transformator liefert dort etwa das 2,5fache seiner Nennleistung.

Maschinentransformatoren sind dauernd belastet, sie werden auf maximalen Wirkungsgrad dimensioniert, d. h., dass bei Nennlast Eisen- und Kupferverluste etwa gleich hoch sind.
Bei einem Ortsnetztransformator, der im Stromnetz verwendet wird, liegt die mittlere Belastungsdauer nur bei ungefähr 40 % der Einschaltdauer, daher können hier höhere Kupferverluste in Kauf genommen werden, während die Eisenverluste stärker reduziert werden. Solche Transformatoren werden hinsichtlich ihres Jahreswirkungsgrades optimiert. Damit wird das Verhältnis der insgesamt pro Jahr primär- und sekundärseitig umgesetzten Energiemengen bezeichnet. Der Jahreswirkungsgrad liegt umso höher, je größer das Verhältnis zwischen Belastungs- und Einschaltdauer ist.

Netzwerkmodellierung

Ersatzschaltbild eines realen Transformators

Die Netzwerkmodellierung eines Transformators verfolgt das Ziel, die wesentlichen nichtidealen Eigenschaften eines Transformators mit einer geringen Zahl an Parametern zu beschreiben. Das nebenstehende Ersatzschaltbild zeigt eine häufig vorgenommene Modellierung mithilfe von linearen Bauelementen. Dabei haben die einzelnen Bauelemente die folgende Bedeutung:

• $U_{p}$: primärseitige Spannungsquelle
• $U_{s}=U_{2}$: Ausgangsspannung
• $I_{1}$, $I_{2}'$: Eingangsstrom und transformierter Ausgangsstrom
• $R_{q1}$: Innenwiderstand der primärseitigen Spannungsquelle
• $L_{\sigma 1}$, $L'_{\sigma 2}$: Streuinduktivität der Primärseite und transformierte Streuinduktivität der Sekundärseite
• $R_{1}$, $R'_{2}$: Wicklungswiderstand der Primärseite und transformierter Wicklungswiderstand der Sekundärseite
• $L_{h1}$: Hauptinduktivität, die den Magnetisierungsstrom führt
• $R_{Fe}$: lineare Modellierung der meist nichtlinearen Eisenverluste im Kern (Fe: Eisen)

Auf die Modellierung der parasitären Kapazitäten der Wicklungen wurde im abgebildeten Modell verzichtet. Ebenso werden nichtlineare Eigenschaften des Transformators nicht abgebildet.

Der eingezeichnete ideale Transformator gehorcht den Transformationsgleichungen:

${\frac {{\underline {U}}_{1}}{{\underline {U}}_{2}}}=\gamma {\text{ und }}{\frac {{\underline {I}}_{1}}{{\underline {I}}_{2}}}={\frac {1}{\gamma }}.$

Der Übertragungsfaktor $\gamma =N_{1}/N_{2}$ bezeichnet dabei das Verhältnis der Windungszahlen von Primär- und Sekundärseite.

Die Größen, die mit einem zusätzlichen Strich ' gekennzeichnet sind, wurden von der Sekundärseite zur Primärseite transformiert. Bei der Transformation einer Impedanz ${\underline {Z}}$ von der Sekundärseite zu einer Impedanz $Z'$ auf der Primärseite gilt die folgende Transformationsgleichung:

${\underline {Z'}}=\gamma ^{2}{\underline {Z}}$

Die Impedanztransformation bedeutet, dass die Eingangsklemmen eines Transformators für einen elektrischen Schaltkreis wie ein Widerstand $\gamma ^{2}\cdot R$ wirken, wenn an die Sekundärseite ein Widerstand R angeschlossen wird. Somit können mithilfe eines Transformators Widerstände vergrößert oder verkleinert werden, indem das Windungsverhältnis $\gamma$ geändert wird.

Die Impedanztransformation wird in elektronischen Schaltungen häufig zur Anpassung eines Netzwerkes an den Wellenwiderstand einer Leitung oder zur Leistungsanpassung eingesetzt. Anders als bei gyratorischer Kopplung bleibt bei transformatorischer Kopplung die Struktur des Netzwerkes erhalten, das heißt Reihen- und Parallelschaltungen bleiben erhalten, und induktives und kapazitives Verhalten werden nicht gegeneinander ausgetauscht.

Wenn es auf die galvanische Trennung des Transformators nicht ankommt, kann der ideale Transformator im Ersatzschaltbild nach Transformation aller sekundärseitigen Bauelemente auf die Primärseite entfallen.

Signalformen und Bandbreite

Die Speisung mit einer sinusförmigen Eingangsspannung ist typisch für Leistungstransformatoren, wie sie beispielsweise im öffentlichen Stromnetz eingesetzt werden. Die Netzfrequenz in einem Stromnetz ist durch die Umdrehungsgeschwindigkeit der Generatoren vorgegeben. Typische Werte für die Netzfrequenz sind 50 Hz (öffentliches Stromnetz in Europa) und 60 Hz (Stromnetz in den USA). In der Bahnstromversorgung gibt es darüber hinaus auch Netze mit Netzfrequenzen von 16,7 Hz und 25 Hz.

In PC-Netzteilen, Frequenzumrichtern und den Wechselrichtern der Photovoltaik werden in speziellen Schaltnetzteilen Rechteckspannungen mit wesentlich höheren Frequenzen erzeugt und transformiert. Die dabei eingesetzten Transformatoren dienen vorwiegend zur galvanischen Trennung und zur Spannungsanpassung, wobei eine Sättigung des Transformatorkerns vermieden wird.

In Sperrwandlern werden zwei magnetisch gekoppelte Spulen mit einem Kern mit Luftspalt als Energiespeicher verwendet. Die über die Primärseite ins magnetische Feld eingebrachte Energie wird nicht sofort entnommen, sondern erst nach Abschalten der Eingangsspannung an der Sekundärseite abgegriffen. Bei rechteckförmigen Eingangsspannungen ergeben sich somit annähernd dreieckförmige Eingangsströme.

Bei der Übertragung von Signalen mit einem Transformator ist es wichtig, dass die Signalanteile aller relevanten Frequenzen übertragen werden. Bei Verwendung einer ohmschen Last weist der Transformator ein sogenanntes Bandpassverhalten auf. Bei ungeeigneter Dimensionierung oder falscher Beschaltung kann ein Transformator darüber hinaus ein unerwünschtes Schwingverhalten, eine sogenannte Resonanzüberhöhung, aufweisen.

Die Begrenzung der Bandbreite nach unten kommt durch die Hauptinduktivität $L_{h1}$ zustande. Sie schließt Signale niedriger Frequenzen kurz. Nach oben erfolgt die Begrenzung der Bandbreite im Netzwerkmodell allein durch die Streuinduktivitäten $L_{\sigma 1}$ und $L_{\sigma 2}$. Ihre Impedanz steigt mit der Frequenz und verhindert auf diese Weise eine Signalübertragung. Bei hohen Frequenzen ist außerdem die kapazitive Kopplung zwischen den einzelnen Windungen relevant.

In der Praxis ist der Frequenzbereich von Transformatoren nach unten vorwiegend durch die erforderliche Größe begrenzt, die mit sinkender Frequenz stark ansteigt. Der typische Frequenzbereich von Niederfrequenztransformatoren reicht bis 16,7 Hz hinunter, der Nennfrequenz für die Bahnstromversorgung. Am oberen Ende des Frequenzbereiches stehen Transformatoren der Hochfrequenztechnik, bei denen die Wicklungen häufig nur noch aus wenigen oder sogar nur einer einzigen Windung bestehen. Die Frequenzspanne handelsüblicher Hochfrequenztransformatoren umfasst einen Bereich von wenigen MHz bis etwa 1 GHz.

Verhalten bei Netzstörungen und beim Einschalten

Verlauf von Strom und Spannung bei Netzstörungen am belasteten Transformator

Typisches Verhalten eines Transformators beim Einschalten. Das Maximum des Magnetisierungsstroms liegt nach der ersten Spannungshalbwelle.

Einschaltvorgänge und Netzstörungen bewirken besonders starke Abweichungen des Transformatorverhaltens vom idealen Verhalten. Beide Vorgänge können den Transformatorkern sättigen und zu beträchtlichen Überströmen führen.

Entsprechend dem Induktionsgesetz entscheidet allein der Verlauf der Eingangsspannung, ob bei einem Transformator Sättigungserscheinungen auftreten oder nicht. Der Belastungszustand spielt keine wesentliche Rolle; selbst ein Kurzschluss auf der Sekundärseite führt nicht zur Sättigung.

Bei einer typischen Netzstörung im 230-V-Netz fallen vereinfacht betrachtet einzelne oder mehrere Spannungshalbwellen beziehungsweise Teile davon aus. Der Transformator reagiert auf das Ausfallen der Netzhalbwelle mit einem großen Sättigungsstrom in der darauf folgenden Halbwelle. Den wesentlichen Beitrag zur Kernsättigung liefert die Vormagnetisierung des Kerns, die durch die Störung der Eingangsspannung verursacht wird.

Beim Abschalten oder Ausfall der Spannung verharrt der Magnetisierungszustand des Kerns in dem Remanenzpunkt, der der Magnetisierung im Abschaltzeitpunkt am nächsten liegt. Abhängig von Polarität und Phasenlage der wiederkehrenden Netzspannung kann das dazu führen, dass ausgehend von diesem Remanenzpunkt der verbleibende Induktionshub bis zur beginnenden Sättigung kleiner ist als die Zeitfläche der wiederkehrenden Spannungshalbwelle. Die durch die Zeitfläche der wiederkehrenden Halbwelle erzwungene Flussänderung im Kern treibt diesen in die Sättigung, wobei große Magnetisierungsströme benötigt werden.

Der ungünstigste Fall für einen Luftkern ist das Einschalten einer vollen Halbwelle, was zum 2-fachen Magnetisierungsstrom des Nennwertes führt. Der ungünstigste Fall für einen Ringkern ist das Einschalten, wenn die Remanenz bei $B=B_{\mathrm {max} }$ liegt und die Polarität der wiederkehrenden Spannung identisch ist mit der vor dem Abschalten. Diesen Verlauf zeigt die untere Prinzipskizze. Der Magnetisierungsstrom ist in diesem Fall im Wesentlichen nur noch durch die Restinduktivität und durch den ohmschen Widerstand der Primärspule und die Impedanz der Netzzuleitung begrenzt. Er kann demnach extreme Werte annehmen, weil der Transformatorkern restlos gesättigt ist und keine Magnetflussänderung mehr aufnehmen kann. Die Sättigungsmagnetisierung spielt auch beim Einschalten des Transformators eine wichtige Rolle; der Einschaltstrom kann dabei kurzzeitig ein Vielfaches des Nennstromes betragen.

Diese Einschaltvorgänge klingen in jedem Fall im Verlauf einiger Halbwellen ab, da aufgrund der Asymmetrie der Magnetisierungsströme auch die beiden gegenpoligen Spannungshalbwellen mit unsymmetrischen Spannungsabfällen behaftet sind. Das hat zur Folge, dass in der Sättigungshalbwelle stets etwas weniger Spannung zur Aufmagnetisierung zur Verfügung steht als bei der dazu gegenpoligen Spannungshalbwelle die zur Abmagnetisierung führt. Dadurch zentriert sich der Magnetisierungs-Schleifendurchlauf selbsttätig nach einigen Netzperioden, wobei die Zeitkonstante dafür aus dem Quotienten der Induktivität dividiert durch die Ohmschen Widerstände im Stromkreis errechnet werden kann. Bei sehr großen Transformatoren kann diese Zeitkonstante deshalb einige Minuten betragen.

Schlienz gibt als Zahlenwert für einen daraufhin optimierten 1,6-kVA-Transformator (230 V), der mit 1 kW belastet wird, einen Strom von 200 A aufgrund der Sättigung an. Im Vergleich dazu fließen im Normalbetrieb weniger als 10 A.

wichtige Seiten

Erste Sätze von Sayda

Sayda verdankt seine Entstehung dem Böhmischen Kämmerer Slauko von Riesenburg. Er ließ hier um 1200 am Böhmischen Steig, einer wichtigen Handelsstraße zwischen Halle und Prag die Straßenburg und eine Zollstätte Saydow gründen. die 1207 erstmals genannt werden.

Im Jahr 1272 wird der zwischenzeitlich entstandene befestigte Ort Zawidow genannt.

Der Name ist altsorbischen Ursprungs und geht auf den Personennamen Zavid zurück, Sayda ist also die Siedlung eines Zavid.

Spätere Schreibweisen des Namens sind Saydowe, Zaydaw, Zaida. 1509 schreibt man erstmalig Sayda

Quelle zu Sayda: 1. urkundl. Erwähnung: [1] Text der Urkunde 2. Quelle: [

nicht unwichtig

Morddrohungen https://de.wikipedia.org/w/index.php?title=Wikipedia:Vandalismusmeldung&action=edit&section=6

Benutzer:ICE21

ICE21 (Diskussion • Beiträge • gelöschte Beiträge • hochgeladene Dateien • SBL-Log • Sperr-Logbuch • globale Beiträge • SUL • Logbuch • sperren)
Moin, der Benutzer wurde am 27. Januar von JD wegen dieses Beitrags (adminonly) für drei Tage gesperrt. Wenige Minuten später initiierte eine IP eine SP, wobei sie in den folgenden Beiträge suizidale Absichten äußerte ([2], [3]). Infolgedessen entsperrte Kulac den Account auf kurzem Dienstweg, was meine volle Unterstützung fand/findet.
Soviel zur Vorgeschichte, denn danach ereigneten sich folgendes:

Unter IP und angemeldet sprach er Drohungen gegen Leib und Leben ([4], [5], [6]) sowie juristischer Natur ([7]), wobei die beiden IPs über das Konfliktfeld Pesterwitz und die vermeintlichen „Gegner“ Striegistaler und Thomas021071 zweifellos ICE21 zuzuordnen sind. Dies wurde zudem auch auf WD:110 diskutiert und die Polizei verständigt (durch Nightflyer, Ping der Vollst. halber). Hinzu kommt noch ein grober Verstoß (adminonly) gegen WP:BIO durch die IP, die die SP initiierte.

Irgendwie scheint das durch die Vorgeschichte untergegangen zu sein, daher bitte ich in Anbetracht der Schwere der Verstöße auch im Nachhinein um eine angemessene Sanktion, auch um diesen Vorgang zu dokumentieren. -- ɦeph 22:11, 11. Feb. 2015 (CET)

Ich hatte es gemeldet, Rückruf erhalten und nichts weiter. Was draus geworden ist, keine Ahnung. Ich bin damit raus. Gruss --Nightflyer (Diskussion) 22:15, 11. Feb. 2015 (CET)

Account unbeschränkt sperren, andere Seiten ggf. halbieren. Offenbar gibt es nichts, was wir sonst tun können. Wenn es denn zweifelsfrei ist. Gibt es einen Beleg? Koenraad 22:27, 11. Feb. 2015 (CET)

Ich war seinerzeit auch beteiligt (siehe: Benutzer_Diskussion:Kulac#Aufhebung_der_Sperre_Benutzer:ICE21). Ich glaube, dass es sich um einen armen Teufel handelt, der Hilfe braucht. Ich weiß aber nicht, was aus der Sache geworden ist. --der Pingsjong (Diskussion) 22:34, 11. Feb. 2015 (CET)

Als Betroffener kündigte ich eine Anzeige an, unternahm aber nichts. Ich dachte ähnlich wie @Pingsjong. Der Teufel ist sicher arm, wahrscheinlich aber auch zu dumm, um die möglichen Folgen seiner Worte einschätzen zu können. Da solche Äußerungen aber ernst genommen werden sollten, plädiere ich auch für eine längere Sperre. Interessant ist natürlich, was aus der Anzeige wird! Falls nichts geschieht wären natürlich Informationen an das Innenministerium und auch an die Medien wünschenswert. Vielen Dank für euren Einsatz --Striegistaler (Diskussion) 22:54, 11. Feb. 2015 (CET)

Sachliche Lösungen

Tach zusammen, das hier hat mich hierher gebracht, und vielleicht kann ich ein wenig zur Klärung beitragen. Ein paar generelle Gedanken:

• Aufgrund der Belegpflicht gilt: "In strittigen Fällen können unbelegte Inhalte von jedem Bearbeiter unter Hinweis auf diese Belegpflicht entfernt werden." Wohlgemerkt: in strittigen Fällen, es sollte also begründbare Zweifel geben. Wer die gelöschten Inhalte wieder drin haben will, muss sie eben belegen.
• In aller Regel gilt: Wissenschaftliche Literatur sticht unwissenschaftliche oder populärwissenschaftliche und neuere wissenschaftliche sticht ältere wissenschaftliche, denn bei solider Wissenschaft darf angenommen werden, dass die älteren Meinungen bewusst nicht übernommen werden.
• Heimatliteratur ist enorm schwierig zu bewerten: Hier gibt es manchmal Hervoragendes und wissenschaftlich Solides, aber genauso oft auch unwissenschaftliche Collagen aus Sagen und überholten Forschungsmeinungen. Meist kann die Zuverlässigkeit heimatkundlicher Literatur ansatzweise wie in der wikipedia selbst abgeschätzt werden: Werden Quellen genannt oder nicht? Was sind das für Quellen: Primärquellen und Archive? Oder noch ältere Literatur?
• Meist ist irrelevant was Stadtverwaltung und Bürgermeister zur Ortsgeschichte sagen, die sind in der Regel weder historisch ausgebildet noch zuständig und mit anderen Aufgaben ausgelastet, es sei denn, es gibt z.B. einen ausgebildeten Stadtarchivar. --UMyd (Diskussion) 16:41, 7. Jul. 2014 (CEST)

Im Prinzip wäre ich bereit. moderierend zu vermitteln. --UMyd (Diskussion) 16:49, 7. Jul. 2014 (CEST)

Danke UMyd, wir sind einer Meinung. Ich will es noch einmal ohne fremde Hilfe versuchen. Ich bin optimistisch. Wenn es schief geht melde ich mich. Ich denke Brainswiffer hat jetzt schon mehrmals gelesen, wie es hier langgeht. Ich möchte gemeinsam mit ihm arbeiten. Freundliche Grüße --Striegistaler (Diskussion) 17:33, 7. Jul. 2014 (CEST)

Überarbeitung notwendig

Der Artikel enthält sprachliche und sachliche Mängel. Ich halte eine gründliche Überarbeitung für notwendig.--Striegistaler (Diskussion) 14:55, 22. Dez. 2013 (CET)

Belege fehlen

Der Artikel enthält nicht oder nicht ausreichend belegte Aussagen. Das gilt insbesondere für die Punkte:

• Urkundliche Ersterwähnung 1185
• Ritter von Nossen und Kloster Altzelle
• Nossen in der Neuzeit -- Striegistaler (Diskussion) 00:46, 26. Jan. 2014 (CET)

Zur meinen Änderungen:

1. Es war seit Januar Zeit, den Text zu korrigieren oder Nachweise zu führen.

2. WP ist kein Märchenbuch

3. auch nicht, wenn das der Heimattümelei Verfallene gern hätten.

4. ich habe den fehlerbehafteten Text wieder gelöscht und durch einen anderen ersetzt. Weitere Belege folgen noch, ich muss um etwas Geduld bitten. --Striegistaler (Diskussion) 09:57, 5. Jul. 2014 (CEST)

Vandalismusmeldung

Hallo Horst Gräbner, du hast meine Nachricht sicher erhalten. Ich habe heute eine VM für Brainswiffer verfasst. Vielleicht kannst du ein Auge auf das Geschehen werfen?

Freundliche Grüße --Striegistaler (Diskussion) 18:56, 5. Jul. 2014 (CEST)

@Striegistaler Etwas verwundert bin ich hierüber schon, da wir ja eigentlich transparent bleiben wollten? Ich erleb(t)e Dich als engagiert und motiviert - aber wir sind bisher meiner Meinung nach immer daran gescheitert, dass Verprechungen und die Realität nicht übereinstimmten. "Wissenschaftlichkeit" beschränkte sich vor allem auf Löschungen (auch von Bequelltem) - ohne dass wirklich entsprechende und bequellte Alternativen kamen (allein die Namensfrage in Nossen als Erinnerung). Ich verstehe oft auch nicht wirklich, worauf Du hinauswillst und ich habe den Verdacht, dass einiges nicht den WIKI-Prinzipien entspricht. Irgendwie reduziere ich alles darauf, dass Du "entdecken" willst, dass die Urkunde, die alle als Erstnachweis für die Stadtgründung 1185 verwenden, dies nicht wirklich sei. Man kann im Rahmen einer OR schon eigene Zweifel vorbringen - nicht aber hier in WP. Ich habe nun hier in Diskussion:Geschichte_der_Stadt_Nossen die Diskussion nochmal präzisiert und schlage nun vor, ausschliesslich dort zu diskutieren - weil die Fragmente auf unseren eigenen Diskussionsseiten schon archiviert sind. So kann zumindest ein Dritter mal in aller Freundschaft auch eine Blick draufwerfen. --Brainswiffer (Disk) 17:21, 6. Jul. 2014 (CEST)

Brainswiffer, das Einzige, was ich "entdeckte", waren gravierende Fehler. Die wollte ich korrigieren. Heute entdeckte ich erstmals von dir versöhnliche Töne. Das lässt hoffen!--Striegistaler (Diskussion) 19:09, 6. Jul. 2014 (CEST)

Ich habe die strittigen Texte angelesen und bin der Meinung, dass sich das lösen lassen sollte. Ich bin bereit, gründlichst zu lesen und gegebenenfalls auch einen Formulierungsvorschlag zu unterbreiten. Allerdings habe ich eine sehr anstrengende Woche hinter mich gebracht und noch eine eben solche vor mir. Zeit und Konzentration werde ich erst Anfang übernächster Woche haben. Falls ihr euch bis dahin nicht habt einigen können, werde ich versuchen, meinen „Senf“ dazu abzugeben. Viele Grüße. --Horst Gräbner (Diskussion) 17:36, 6. Jul. 2014 (CEST)

Danke, nimm dir Zeit. Ich werde noch ein letztes Mal versuchen, einvernehmlich Bockmist wegzuräumen. Ich muss mich nicht wie ein kleines Kind von einem die Fakten und Vorgänge nicht Kennenden abtoffeln lassen. Es ist schon ziemlich dreist, sich auf Nossen-Historiker zu beziehen, ohne den sehr guten Artikel in der Festschrift „825 Jahre Nossen“ von 2010 zu kennen. Bisher habe ich, auch ohne den Artikel von Dr. Michael Lindner zu kennen (zum Teil auch erfolgreich) versucht, das einzufügen, was auch er schreibt. Ich habe das gelöscht was z. B. eben nicht in der Urkunde steht, was auch nicht mit Primärquellen belegbar ist. Das wird mir zum Vorwurf gemacht. Zu Einfügen des neuen Textes hatte ich überhaupt zu wenig Zeit, alles war revertiert.

Hier die Liste der Publikationen von Lindner: http://opac.regesta-imperii.de/lang_de/autoren.php?name=Lindner%2C+Michael, damit du dir ein Bild über die Person machen kannst, mit dessen Darstellung der Geschichte von Nossen ich voll inhaltlich übereinstimme, abgesehen von wenigen kleinen subjektiven Schlussfolgerungen.

Viele freundliche Grüße sendet der --Striegistaler (Diskussion) 19:09, 6. Jul. 2014 (CEST)

Schon die Bewertungen und PA in diesem Beitrag lassen mich nichts Gutes ahnen :-) MoM geht hier fast immer schief. --Brainswiffer (Disk) 20:00, 6. Jul. 2014 (CEST)

Striegistaler - Brainswiffer

Armin P., Brainswiffer verfolgt hier jeden meiner Schritte, auch das was ich jetzt schreibe, wird er bald wissen. Zunächst noch einmal vielen Dank. Wir sind (unter Vorbehalt) einer Meinung. Bei meiner VM gegen Brainswiffer bat ich, dass ein der spätmittelalterlichen möglichst sächsischen Geschichte Kundiger einen Blick auf unseren unsäglichen Streit lenkt. Nun scheint mein Wunsch auf anderem Weg (wenigstens teilweise?) in Erfüllung gegangen zu sein. Unser Streit erstreckt sich über lange Zeit, wurde auf allen relevanten Diskussionsseiten geführt, es gab auch private E-Mail-Kontakte. Ich will das nicht wieder aufwärmen. Allein die Ereignisse der letzten Tage sollten reichen, sich ein Bild über die beiden Streithähne zu machen. Es wäre mir sehr angenehm, wenn du dich dieser Sache annehmen könntest. Ich bat auch schon Horst Gräbner, der hat momentan aber wenig Zeit, ich weiß auch nicht, ob er fachkundig ist. Ich würde mich nicht wundern wenn, wenn sich Brainswiffer auch hier mit einem Kommentar meldet. Ich wünsche dir noch einen schönen Tag --Striegistaler (Diskussion) 13:18, 7. Jul. 2014 (CEST)

Wenn der Streit über längere Zeit geht, ist es für einen Außenstehenden kaum möglich dort moderierend einzugreifen, weil die Fronten einfach verhärtet sind. Der ganze Artikel Geschichte der Stadt Nossen ist auf jeden Fall stark überarbeitungsbedürftig und würde großen Aufwand an Zeit erfordern ihn auf vernünftiges Niveau zu bringen. So zitiert man jedenfalls keine Literatur:

• Sonderdruck aus: Höfe und Residenzen im spätmittelalterlichen Reich. Ein dynastisch-topographisches Handbuch (= Residenzenforschung, Bd. 15.I). ISBN 3-7995-4515-8 © Jan Thorbecke Verlag, Ostfildern
• S.16 "825 Jahre Nossen- Festschrift zum Jubiläum"
• S.24 "825 Jahre Nossen- Festschrift zum Jubiläum"

Den Inhalt möchte ich mir dann schon gar nicht mehr ansehen. Vielleicht solltet ihr eine Schlichtungsstelle in wikipedia bemühen? Ansonsten gibt es auch noch die WP:Redaktion Geschichte. Wünsche ebenfalls noch einen schönen Tag. --Armin (Diskussion) 15:12, 7. Jul. 2014 (CEST)

Danke, ich glaube eine Moderation wird nicht mehr notwendig sein. Ich werde Brainswiffer deine Worte mitteilen, er hat sich in den letzten Nachrichten schon sehr gemäßigt. Ich machte schon den Vorschlag - weil wesentlich einfacher - den Text neu zu schreiben. Über den Stand der VM bin ich nicht informiert, ist das schon erledigt? Falls nicht will ich die weitere Kooperationsbereitschaft abwarten, dann den Antrag auf Erledigung stellen. Ich wünsche dir einen schönen Abend. --Striegistaler (Diskussion) 15:48, 7. Jul. 2014 (CEST)

Über die Anfänge und die ersten Jahrhunderte von Gersdorf gibt es keine schriftlichen Zeugnisse. Die erste urkundliche Erwähnung erfolgte im Jahr 1502 als Gerßdorf (1541 erwähnt als Girßdorff, auch Girsdorff). Die Herkunft und die ursprüngliche Bedeutung des Namens sind ungewiss; es wird vermutet, dass ein Zusammenhang mit einem Personennamen, der mit Ger- beginnt, besteht. Nachweisbar ist für das Jahr 1200 ein gewisser Gerhardus, der 1216 bis 1224 Abt des Klosters Altzella war.

Die Mehrzahl der Dörfer der Klosterstiftung waren Bauerndörfer, die von Markgraf Otto oder Tammo von Strehla gegründet wurden (Quelle?). Gersdorf wird in diesem Zusammenhang nicht erwähnt, ebenso wie für den Ort keine Waldhufenflur nachweisbar ist. (Quelle?). Die nach Osten lückenlos an Gersdorf anschließenden Ortschaften Kummersheim und Kaltenborn sind als Klostervorwerke am steil abfallendem Gelände zur Freiberger Mulde belegt (Quelle?). Für Gersdorf liegt kein entsprechender Beleg vor, allerdings ist eine andere Grundherrschaft ebenfalls nicht nachweisbar.<<

+ :::Damit sind keine „Vermutungen“ geäußert, sie ergeben sich praktisch/logisch aus der Formulierung. Geschildert sind nur belegbare Fakten.

 + :::Grüßchen. --Horst Gräbner (Diskussion) 22:45, 25. Aug. 2014 (CEST)