Liste von Kartennetzentwürfen
Zur Navigation springen
Zur Suche springen
Dies ist eine chronologisch sortierte Liste von Kartennetzentwürfen, die eigene Artikel auf Wikipedia haben oder anderweitig bemerkenswert sind. Da die Anzahl der möglichen Kartenprojektionen nicht begrenzt ist,[1] kann es keine umfassende Liste geben.
Erläuterungen
[Bearbeiten | Quelltext bearbeiten]Projektionstyp
[Bearbeiten | Quelltext bearbeiten]- Zylindrisch
- In der Standarddarstellung bilden diese regelmäßig beabstandete Meridiane zu gleichmäßig beabstandeten vertikalen Linien und Parallelen zu horizontalen Linien ab.
- Pseudozylindrisch
- In der Standarddarstellung bilden diese den Zentralmeridian und die Parallelen als gerade Linien ab. Andere Meridiane sind Kurven (oder möglicherweise gerade vom Pol zum Äquator), die regelmäßig entlang von Parallelen verlaufen.
- Konisch / Kegelförmig
- In der Standarddarstellung bilden konische (oder kegelförmige) Projektionen Meridiane als Geraden und Parallelen als Kreisbögen ab.
- Pseudokonisch
- In der Standarddarstellung stellen pseudokonische Projektionen den Zentralmeridian als gerade Linie, andere Meridiane als komplexe Kurven und Parallelen als Kreisbögen dar.
- Azimutal
- In der Standarddarstellung stellen azimutale Projektionen Meridiane als Geraden und Parallelen als vollständige, konzentrische Kreise dar. Sie sind radial symmetrisch. In jeder Darstellung (oder in jedem Aspekt) bewahren sie Richtungen vom Mittelpunkt aus. Das bedeutet, dass Großkreise durch den Mittelpunkt durch Geraden auf der Karte dargestellt werden.
- Pseudoazimutal
- In der Standarddarstellung bilden pseudoazimutale Projektionen den Äquator und den Zentralmeridian auf senkrechte, sich schneidende Geraden ab. Sie bilden Parallelen zu komplexen Kurven ab, die vom Äquator weg verlaufen, und Meridiane zu komplexen Kurven, die zum Zentralmeridian hin verlaufen. Hier nach pseudozylindrisch aufgelistet, da sie ihnen in Form und Zweck im Allgemeinen ähnlich sind.
- Retroazimutal
- Die Richtung zu einem festen Punkt B (auf dem kürzesten Weg) entspricht der Richtung auf der Karte von A nach B.
- Andere
- Typischerweise aus einer Formel berechnet und nicht auf einer bestimmten Projektion basierend.
- Polyhedral
- Polyedrische Karten können zu einer polyedrischen Annäherung an die Kugel gefaltet werden, wobei eine besondere Projektion verwendet wird, um jede Fläche mit geringer Verzerrung abzubilden.
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]- Konform
- Bewahrt die Winkel lokal, was bedeutet, dass lokale Formen nicht verzerrt werden und dass der lokale Maßstab in allen Richtungen von jedem gewählten Punkt aus konstant ist.
- Flächentreu
- Das Flächenmaß bleibt überall erhalten.
- Kompromiss
- Weder konform noch flächentreu, sondern ein Gleichgewicht, das die Gesamtverzerrung reduzieren soll.
- Äquidistant
- Alle Abstände von einem (oder zwei) Punkten sind korrekt. Andere äquidistante Eigenschaften werden in den Anmerkungen erwähnt.
- Gnomonisch
- Alle Großkreise sind Geraden.
Tabelle chronologisch
[Bearbeiten | Quelltext bearbeiten]| Abbildung | Jahr | Projektion | Urheber | Typ | Eigenschaften | Anmerkungen |
|---|---|---|---|---|---|---|
 |
580 v. Chr. (ca.) | gnomonische Projektion | Thales (möglicherweise) |
azimutal | gnomonisch | Alle Großkreise werden auf Geraden abgebildet, extreme Verzerrung weit vom Zentrum entfernt; zeigt weniger als eine Hemisphäre. |
 |
200 v. Chr. (ca.) | stereografische Projektion | Hipparchos * (veröffentlicht) |
azimutal | konform | Die Karte ist unendlich groß und die äußere Hemisphäre bläht sich stark auf, so dass sie oft als zwei Hemisphären verwendet wird. Kartografiert alle kleinen Kreise zu Kreisen, was für die planetarische Kartierung nützlich ist, um die Formen von Kratern zu erhalten. |
 |
200 v. Chr. (ca.) | orthografische Azimutalprojektion | Hipparchos * (veröffentlicht) |
azimutal | Blick aus unendlicher Entfernung | |
 |
100 (ca.) | längentreue Kegelprojektion = (äquidistante od. auch isometrische) = einfach kegelförmig |
basierend auf der ersten Projektion von Claudius Ptolemäus | konisch | flächentreu | Die Entfernungen entlang der Meridiane bleiben ebenso erhalten wie die Entfernungen entlang einer oder zwei Standardparallelen.[2] |
 |
120 (ca.) | Plattkarte oder rektanguläre bzw. rektangulare Projektion = Rektangularprojektion = parallelogrammatische Karte |
Marinos von Tyros | zylindrisch | flächentreu | einfachste Geometrie; Entfernungen entlang der Meridiane bleiben erhalten quadratische Plattkarte: Spezialfall mit dem Äquator als Standardparallele |
 |
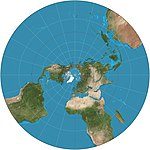
1000 (ca.) | mittabstandstreue Azimutalprojektion | Abū Rayḥān al-Bīrūnī | azimutal | flächentreu | Entfernungen vom Zentrum bleiben erhalten. Wird als Emblem der Vereinten Nationen verwendet, das bis 60° S reicht. Wird vom USGS im Nationalatlas der Vereinigten Staaten von Amerika verwendet. |
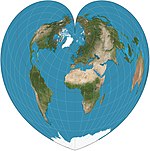 |
1500 (ca.) | Stab-Wernersche Projektion = Werner-Projektion |
Johannes Stabius | pseudokonisch | flächentreu, äquidistant | Parallelen sind gleich beabstandete konzentrische Kreisbögen. Die Abstände vom Nordpol sind korrekt, ebenso wie die gekrümmten Abstände entlang der Parallelen und die Abstände entlang des Zentralmeridians. |
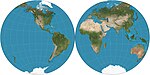 |
1000 (ca.), 1660 | Nicolosi-Kugelprojektion | Abū Rayḥān al-Bīrūnī, neu erfunden 1660 von Giovanni Battista Nicolosi | pseudokonisch[3] | Kompromiss | |
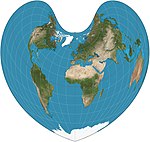 |
1511 | Bonnesche Projektion | Bernardus Sylvanus | pseudokonisch, herzförmig | flächentreu | Parallelen sind gleich beabstandete konzentrische Kreisbögen und Standardlinien. Das Aussehen hängt von der Referenzparallele ab. Allgemeiner Fall von Werner-Proj. und sinusförmig. |
 |
1514 | Oktanten-Projektion | Leonardo da Vinci | polyhedral | Kompromiss | projiziert den Globus auf acht Oktanten (Reuleaux-Dreiecke) ohne Meridiane und ohne Parallelen |
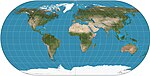 |
1540 | Ortelius ovale Projektion | Battista Agnese | pseudozylindrisch | Kompromiss | Meridiane sind kreisförmig.[4] |
 |
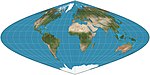
1569 | Mercator-Projektion = Wright |
Gerhard Mercator | zylindrisch | konform | Linien mit konstanter Peilung (Loxodrome) sind gerade, was die Navigation von Seeschiffen erleichtert. Die Gebiete blähen sich mit dem Breitengrad auf und werden so extrem, dass die Karte die Pole nicht mehr anzeigen kann. |
 |
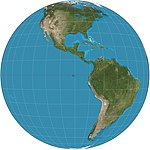
1570 (ca.) | Sinusoidal-Projektion = Sanson-Flamsteed = Mercator flächentreu |
(mehrere; der Erste ist unbekannt) | pseudozylindrisch | flächentreu, äquidistant | Meridiane sind Sinuskurven; Parallelen sind in gleichen Abständen angeordnet. Das Seitenverhältnis beträgt 2:1. Die Abstände entlang der Parallelen sind konserviert. Jean Cossin von Dieppe war einer der ersten Kartographen, der das Sinusoidale verwendete, das in einer Weltkarte von 1570 erschien.[5] |
 |
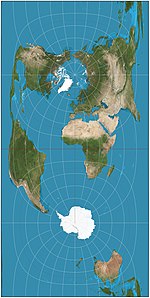
1740 | Vertikal-Perspektive | Matthäus Seutter * |
azimutal | Ansicht aus einer endlichen Entfernung, kann nur weniger als eine Hemisphäre darstellen. | |
 |
1745 | Cassini-Projektion = Cassini–Soldner |
César François Cassini de Thury | zylindrisch | äquidistant | quer zur äquidistanten Projektion; die Abstände entlang des Zentralmeridians sind konserviert. Distanzen senkrecht zum Zentralmeridian bleiben erhalten. |
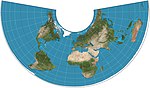
| 1772 | Lamberts Zylinderprojektion | Johann Heinrich Lambert | zylindrisch | flächentreu | Standardparallele am Äquator, Seitenverhältnis von π (3,14). Grundprojektion der zylindrischen Gleichflächenfamilie. | |
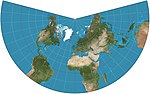 |
1772 | Lamberts winkeltreue Kegelprojektion | Johann Heinrich Lambert | konisch | konform | wird in Luftfahrtkarten verwendet |
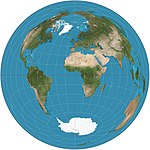 |
1772 | flächentreue Azimutalprojektion | Johann Heinrich Lambert | azimutal | flächentreu | Die geradlinige Entfernung zwischen dem zentralen Punkt auf der Karte und einem beliebigen anderen Punkt ist gleich der geradlinigen 3D-Entfernung durch den Globus zwischen den beiden Punkten. |
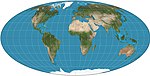 |
1805 | Mollweide-Projektion = elliptisch = Babinet = homolographisch |
Carl Brandan Mollweide | pseudozylindrisch | flächentreu | Meridiane sind Ellipsen. |
 |
1805 | Albers-Kegelprojektion | Heinrich Christian Albers | konisch | flächentreu | zwei Standardparallelen mit geringer Verzerrung zwischen ihnen. |
 |
1820 (ca.) | amerikanische polykonische Projektion | Ferdinand Rudolph Hassler | pseudokonisch | Kompromiss | Die Entfernungen entlang der Parallelen bleiben ebenso erhalten wie die Entfernungen entlang des Zentralmeridians. |
 |
1822 | Gauss-Krüger-Projektion = Gauss-Konform = (ellipsoidal) transversale Mercator-Proj. |
Carl Friedrich Gauss Johann Heinrich Louis Krüger |
zylindrisch | konform | Diese transversale, ellipsoide Form des Mercator-Entwurfs ist endlich, im Gegensatz zur äquatorialen Mercator-Projektion. Sie bildet die Grundlage der universalen transversalen Mercator-Projektion. |
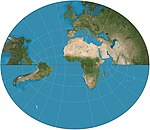 |
1833 | Littrow-Projektion | Joseph Johann von Littrow | retroazimutal | konform | Auf der äquatorialen Seite zeigt es eine Halbkugel mit Ausnahme der Pole. |
 |
1850 (ca.) | zentral-zylindrische Projektion | (unbekannt) | zylindrisch | Perspektive | In der Kartographie wegen der starken Polarverzerrung praktisch unbenutzt, aber in der Panoramafotografie beliebt, insbesondere für Architekturszenen. |
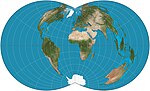 |
1853 (ca.) | rechteckige polykonische Projektion | National Geodetic Survey | pseudokonisch | Kompromiss | Es kann der Breitengrad gewählt werden, entlang dem der Maßstab korrekt ist; Parallelen treffen rechtwinklig auf Meridiane. |
 |
1855 | stereografische Projektion von Gall ähnlich der stereografischen Projektion von Braun |
James Gall | zylindrisch | Kompromiss | Sie sollte dem Mercator-Entwurf ähneln und gleichzeitig die Pole zeigen, Standardparallelen bei 45° N/S. |
 |
1855[6] | Gall-Peters-Projektion = Gall’s Orthographic Projection = Peters |
James Gall (Arno Peters) | zylindrisch | flächentreu | Horizontal komprimierte Version der Lambert-Zylinderprojektion. Standardparallelen bei 45°N/S. Seitenverhältnis von ~1,6. Ähnlich ist die Balthasart-Projektion mit Standardparallelen bei 50° N/S. Karten, die auf der Projektion basieren, werden von der UNESCO gefördert, sie werden von britischen Schulen häufig verwendet.[7] |
| 1865 (ca.) | Collignon-Projektion | Édouard Collignon | pseudozylindrisch | flächentreu | Je nach Konfiguration kann die Projektion die Kugel auch auf einen einzelnen Diamanten oder ein Paar von Quadraten abbilden. | |
 |
1879 | Quincunx-Kartenprojektion | Charles Sanders Peirce | andere | konform | Mosaike. Können kontinuierlich auf einer Ebene gekachelt werden, wobei die Kantenübergänge bis auf vier einzelne Punkte pro Kachel übereinstimmen. |
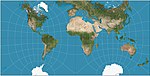 |
1887 | Guyou-Halbkugel-im-Quadrat-Projektion | Émile Guyou | andere | konform | Mosaike |
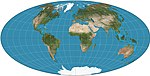 |
1889 | Aitov-Projektion | Dawid Alexandrowitsch Aitow | pseudoazimutal | Kompromiss | Dehnung der modifizierten äquatorialen azimutalen Äquidistanzkarte. Die Grenze ist eine 2:1-Ellipse. Wurde weitgehend von Hammer abgelöst. |
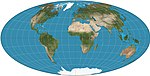 |
1892 | Hammer-Projektion = Hammer-Aitoff Variationen: Briesemeister |
Ernst von Hammer | pseudoazimutal | flächentreu | Basiert auf der Aitov-Projektion, geändert gegenüber der azimutalen äquatorialen flächentreuen Äquatorialkarte. Die Grenze ist eine 2:1-Ellipse. Varianten sind schräge Versionen, zentriert auf 45° N. |
 |
1903 | Hotine's schiefer Mercator | M. Rosenmund, J. Laborde, Martin Hotine | zylindrisch | konform | |
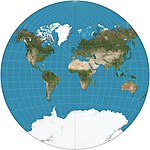 |
1904 | Van-der-Grinten-Projektion | Alphons J. van der Grinten | andere | Kompromiss | Die Grenze ist ein Kreis. Alle Parallelen und Meridiane sind Kreisbögen. Gewöhnlich nahe 80° N/S beschnitten. Standard-Weltprojektion der NGS in den Jahren 1922–1988. |
 |
1906 | Eckert-I- und Eckert-II-Projektion | Max Eckert-Greifendorff | pseudozylindrisch | flächentreu | |
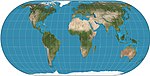 |
1906 | Eckert-III- und Eckert-IV-Projektion | Max Eckert-Greifendorff | pseudozylindrisch | flächentreu | Parallelen sind in Abstand und Maßstab ungleich; äußere Meridiane sind Halbkreise, andere Meridiane sind Halbellipsen. |
 |
1906 | Eckert-V- und Eckert-VI-Projektion | Max Eckert-Greifendorff | pseudozylindrisch | flächentreu | Parallelen sind in Abstand und Maßstab ungleich; Meridiane sind Halbperioden-Sinuskurven. |
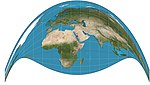 |
1909 | Craig-Retroazimutal-Projektion = Mekka-Projektion |
James Ireland Craig | retroazimutal | Kompromiss | Es handelt sich um eine modifizierte zylindrische Projektion. |
 |
1909 | Cahills Schmetterlingskarte | Bernard Joseph Stanislaus Cahill | polyhedral | Kompromiss | Projiziert den Globus auf ein Oktaeder mit symmetrischen Komponenten und aneinander grenzenden Landmassen, die in verschiedenen Anordnungen dargestellt werden können. |
 |
1910 | Hammer-Retroazimutal-Projektion, vordere Hemisphäre | Ernst von Hammer | retroazimutal | ||
 |
1910 | Hammer-Retroazimutal-Projektion, hintere Hemisphäre | Ernst von Hammer | retroazimutal | ||
 |
1910 | Behrmann-Projektion | Walter Behrmann | zylindrisch | flächentreu | Horizontal komprimierte Version der Lamberts Zylinderprojektion, hat Standardparallelen bei 30° N/S und ein Seitenverhältnis von 2,36. |
 |
1919 | Zwei-Punkt-Äquidistanzprojektion | Hans Maurer | azimutal | äquidistant | Zwei „Passpunkte“ können fast willkürlich gewählt werden. Die beiden geradlinigen Entfernungen von einem beliebigen Punkt auf der Karte zu den beiden Passpunkten sind korrekt. |
 |
1921 | Winkel-Tripel-Projektion | Oswald Winkel | pseudoazimutal | Kompromiss | Arithmetisches Mittel der Plattkarte und der Aitoff-Projektion; Standard-Weltprojektion für die NGS seit 1998. |
| 1922 | Roussilhe's schräge stereographische Projektion | Henri Roussilhe | ||||
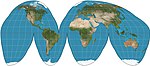 |
1923 | Goode-Projektion | John Paul Goode | pseudozylindrisch | flächentreu | Hybrid aus Sinusoidal- und Mollweide-Projektion, normalerweise in unterbrochener Form verwendet. |
 |
1925 | Adams-Halbkugel im Quadrat | Oscar Sherman Adams | andere | Konform | |
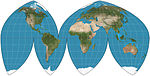 |
1929 | Boggs eumorphe Projektion | Samuel Whittemore Boggs | pseudozylindrisch | flächentreu | Die flächentreue Projektion, die sich aus dem Mittelwert der Sinusoidal- und Mollweide y-Koordinaten ergibt und dadurch die x-Koordinate einschränkt. |
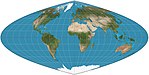 |
1929 | Craster parabolisch =Reinhold Putniņš P4 |
John Craster | pseudozylindrisch | flächentreu | Meridiane sind Parabeln. Standardparallelen bei 36°46′ N/S; Parallelen sind in Abstand und Maßstab ungleich; 2:1 Aspekt. |
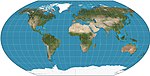 |
1932 | Wagner-VI-Projektion | K. H. Wagner | pseudozylindrisch | Kompromiss | Äquivalent zu Kawraiski VII vertikal um den Faktor komprimiert. |
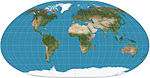 |
1935, 1966 | Loximutale Projektion | Karl Siemon, Waldo Rudolph Tobler | pseudozylindrisch | Von der angegebenen Mitte aus sind die Linien konstanter Peilung (Loxodrome) gerade und haben die richtige Länge; im Allgemeinen asymmetrisch um den Äquator. | |
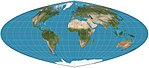 |
1937, 1944 | quartische authalische Projektion | Karl Siemon Oscar Adams |
pseudozylindrisch | flächentreu | Die Parallelen sind ungleichmäßig in Abstand und Maßstab, keine Verzerrung entlang des Äquators, Meridiane sind Kurven vierter Ordnung. |
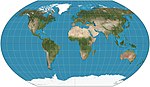 |
1939 | Kawraiski-VII-Projektion | Wladimir Wladimirowitsch Kawraiski | pseudozylindrisch | Kompromiss | Gleichmäßig verteilte Parallelen. Äquivalent zu Wagner VI horizontal um den Faktor komprimiert. |
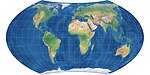 |
1941 | Wagner-VII-Projektion = Hammer-Wagner |
K. H. Wagner | pseudozylindrisch | flächentreu | |
 |
1942 | Miller-Zylinderprojektion | Osborn Maitland Miller | zylindrisch | Kompromiss | Sie sollte dem Mercator-Entwurf ähneln und gleichzeitig die Pole zeigen. |
 |
1943 | Dymaxion-Projektion = Fuller-Projektion |
Richard Buckminster Fuller | polyhedral | Kompromiss | Weltkarte auf der Oberfläche eines Ikosaeders, die sich entfalten und auf zwei Dimensionen abflachen lässt. Die flache Karte ist stark unterbrochen, um Formen und Größen zu erhalten. |
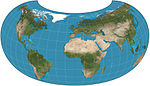 |
1943 | Armadillo-Projektion | Erwin Raisz | andere | Kompromiss | |
 |
1948 | Atlantis-Projektion = Mollweide transverse |
John Bartholomew | pseudozylindrisch | flächentreu | schräge Version der Mollweide-Projektion |
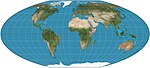 |
1949 | McBryde–Thomas flachpolar-quartic = McBryde-Thomas #4 |
Felix W. McBryde, Paul Thomas | pseudozylindrisch | flächentreu | Standardparallelen bei 33°45′ N/S; Parallelen sind in Abstand und Maßstab ungleich; Meridiane sind Kurven vierter Ordnung; verzerrungsfrei nur dort, wo die Standardparallelen den Zentralmeridian schneiden. |
 |
1951 | Hölzel-Projektion = Hölzel-Planisphäre |
Verlag Ed. Hölzel | pseudozylindrisch | Mit ungleich langen parallel gleichabständig verlaufenden Breitengraden, wobei die Pole in Form einer Polarlinie dargestellt werden. Die Längenkreise werden bis zu einer Breite von 80° als Sinuskurven dargestellt, und weiter nördlich ellipsoid zum Pol geführt. Sie ist weder winkeltreu (konform) noch flächentreu, und kein Punkt der Karte ist verzerrungsfrei. Variante der Eckert-V-Projektion; für den Kozenn-Atlas von 1951 erstmals verwendet und in Österreich bis heute verbreitet. | |
 |
1953 | Bertin-Projektion = Bertin-Rivière = Bertin 1953 |
Jacques Bertin | andere | Kompromiss | Projektion, bei der der Kompromiss nicht mehr homogen ist, sondern für eine größere Deformation der Ozeane modifiziert wird, um eine geringere Deformation der Kontinente zu erreichen. Häufig für französische geopolitische Karten verwendet.[8] |
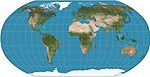 |
1963 | Robinson-Projektion | Arthur H. Robinson | pseudozylindrisch | Kompromiss | Berechnet durch Interpolation von tabellarischen Werten. Wird von Rand McNally seit seiner Gründung verwendet und von der NGS in den Jahren 1988–1998 eingesetzt. |
| 1963 | Breitenmäßig gleich differentielle polykonische Projektion | China State Bureau of Surveying and Mapping | pseudokonisch | Kompromiss | Polykonisch: Parallelen sind nicht konzentrische Kreisbögen. | |
 |
1965 | The Times | John Muir | pseudozylindrisch | Kompromiss | Standardparallelen 45° N/S. Parallelen auf der Grundlage der Gallischen Stereographie, aber mit gekrümmten Meridianen. Entwickelt für Bartholomew Ltd., The Times Atlas. |
 |
1965 | Lee-konforme Welt in einem Tetraeder | L. P. Lee | polyhedral | Konform | Projiziert den Globus auf einen regelmäßigen Tetraeder. Mosaike. |
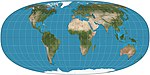 |
1973 | Tobler-Hyperelliptische Projektion | Waldo Rudolph Tobler | pseudozylindrisch | flächentreu | Eine Familie von Kartenprojektionen, die als Sonderfälle die Mollweide-Projektion, die Collignon-Projektion und die verschiedenen zylindrischen flächengleichen Projektionen umfasst. |
| 1973 | vierseitiger sphärischer Würfel | F. Kenneth Chan, E. M. O’Neill | polyhedral | flächentreu | ||
 |
1975 | Cahill-Keyes-Projektion | Gene Keyes | polyhedral | Kompromiss | Projiziert den Globus auf ein abgestumpftes Oktaeder mit symmetrischen Komponenten und aneinandergrenzenden Landmassen, die in verschiedenen Anordnungen dargestellt werden können. |
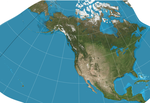 |
1982 | GS50-Projektion | John P. Snyder | andere | konform | Speziell entwickelt, um Verzerrungen zu minimieren, wenn alle 50 US-Bundesstaaten angezeigt werden. |
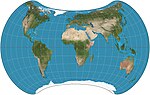 |
1994 | Strebe-1995-Projektion | Daniel „daan“ Strebe | pseudoazimutal | flächentreu | Formuliert unter Verwendung anderer flächentreuer Kartenprojektionen als Transformationen. |
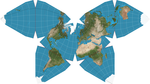 |
1996 | Waterman-Schmetterlingsprojektion | Steve Waterman | polyhedral | Kompromiss | Projiziert den Globus auf ein abgestumpftes Oktaeder mit symmetrischen Komponenten und aneinander grenzenden Landmassen, die in verschiedenen Anordnungen dargestellt werden können. |
 |
1997 | HEALPix | Krzysztof M. Górski | pseudozylindrisch | flächentreu | Hybrid aus Collignon + Lamberts Zylinderprojektion |
 |
1999 | Authagraph-Projektion | Hajime Narukawa | polyhedral | Kompromiss | Annähernd flächentreu. Mosaike. |
 |
2002 | Hobo-Dyer-Projektion | Mick Dyer | zylindrisch | flächentreu | Horizontal komprimierte Version der Lamberts Zylinderprojektion. Sehr ähnlich sind Trystan-Edwards- und Smyth-Gleichflächenprojektionen (= Craster-Rechteck) mit Standardparallelen bei etwa 37° N/S. Seitenverhältnis von ~ 2.0. |
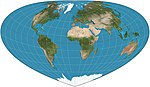 |
2003 | Bottomley-Projektion | Henry Bottomley | pseudokonisch | flächentreu | Alternative zur Bonneschen Projektion mit einfacherer Gesamtform Parallelen sind elliptische Bögen. Das Erscheinungsbild hängt von der Referenzparallele ab. |
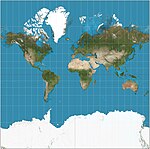 |
2005 | Web Mercator-Projektion | zylindrisch | Kompromiss | Mercator-Variante, die die Elliptizität der Erde für schnelle Berechnungen ignoriert und die Breitengrade für Präsentationen auf etwa 85,05° reduziert. De-facto-Standard für Web-Mapping-Anwendungen. Sie wird von praktisch allen großen Online-Kartenanbietern verwendet, darunter Google Maps, Mapbox,[9] Bing Maps, OpenStreetMap, Mapquest, Esri, und viele andere.[10] | |
| 2008 | Myriahedrale Projektionen | Jarke J. van Wijk | polyhedral | flächentreu | Projiziert den Globus auf ein Myriahedron: ein Polyeder mit einer sehr großen Anzahl von Gesichtern.[11][12] | |
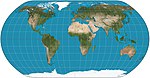 |
2011 | Projektion Natural Earth | Tom Patterson | pseudozylindrisch | Kompromiss | berechnet durch Interpolation von tabellarischen Werten |
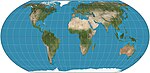 |
2018 | Projektion Equal Earth | Bojan Šavrič, Tom Patterson y Bernhard Jenny | pseudozylindrisch | flächentreu | Inspiriert von der Robinson-Projektion, behält aber die relative Größe der Flächen bei. |
* Der erste bekannte Popularisierer/Nutzer und nicht unbedingt der Urheber.
Literatur
[Bearbeiten | Quelltext bearbeiten]- John P. Snyder: Map projections – A working manual (= U.S. Geological Survey Professional Paper. Band 1395). U.S. Government Printing Office, Washington, D.C. 1987, Map projections: A working manual, doi:10.3133/pp1395 (usgs.gov [PDF; abgerufen am 4. August 2020]).
- John P. Snyder, Philip M. Voxland: An Album of Map Projections (= U.S. Geological Survey Professional Paper. Band 1453). U.S. Government Printing Office, Washington, D.C. 1989, doi:10.3133/pp1453 (usgs.gov [PDF; abgerufen am 4. August 2020]).
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Snyder, John P.: Flattening the earth: two thousand years of map projections. University of Chicago Press, 1993, ISBN 0-226-76746-9, S. 1.
- ↑ Furuti, Carlos A. Conic Projections: Equidistant Conic Projections
- ↑ Archivierte Kopie ( vom 29. April 2016 im Internet Archive)
- ↑ Donald Fenna: Cartographic Science: A Compendium of Map Projections, with Derivations. CRC Press, 2006, ISBN 978-0-8493-8169-0, S. 249 (google.com).
- ↑ Jean Cossin, Carte cosmographique ou Universelle description du monde avec le vrai traict des vents, 1570.
- ↑ Gall wird das Verdienst zugeschrieben, die Projektion 1855 auf einem Wissenschaftskongress beschrieben zu haben.
- ↑ Higgins, Hannah B. The Grid Book. Cambridge, Massachusetts: MIT Press, 2009, ISBN 978-0-262-51240-4; S. 94. „Embroiled in controversy from the start, the map is nonetheless widely used in the British school system and is promoted by the United Nations Educational and Scientific Cultural Organization (UNESCO) because of its ability to communicate visually the actual relative sizes of the various regions of the planet.“
- ↑ Philippe Rivière: Bertin Projection (1953). In: visionscarto. 1. Oktober 2017, abgerufen am 27. Januar 2020.
- ↑ Our Map Data. MapBox, abgerufen am 20. Juni 2018: „Mapbox supports the popular Web Mercator projection, and currently does not support any other projections for display.“
- ↑ Sarah E. Battersby, Michael P. Finn, E. Lynn Usery, Kristina H. Yamamoto: Implications of Web Mercator and Its Use in Online Mapping. In: Cartographica. 49. Jahrgang, Nr. 2, 2014, S. 92, doi:10.3138/carto.49.2.2313 (usgs.gov [PDF]).
- ↑ Jarke J. van Wijk: Unfolding the Earth: Myriahedral Projections. [1]
- ↑ Carlos A. Furuti: Interrupted Maps: Myriahedral Maps. [2]
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Beschreibung der verschiedenen Kartenprojektionen (Links zu jeder Projektion auf der linken Seite der Seite - auf Englisch)
- Liste der Kartenprojektionen (mit Beispielen) (auf Englisch)
- Visuelle Kartenprojektionsliste
