Reduzierbarer und irreduzierbarer Kontrollflussgraph
Die Menge der Kontrollflussgraphen kann in reduzierbare und irreduzierbare Kontrollflussgraphen partitioniert (geteilt) werden. Diese Einteilung geht auf Frances E. Allen zurück.[1] Hecht und Ullman geben äquivalente Charakterisierungen zu Allens ursprünglicher Definition und benutzen diese, um zu zeigen, dass strukturierte Kontrollstrukturen stets reduzierbare Kontrollflussgraphen erzeugen.[2] Eine Auflistung alternativer Charakterisierungen findet sich in einer späteren Veröffentlichung.[3]
Ein für die Definition eines reduzierbaren Kontrollflussgraphen wichtiger Begriff ist der einer Rückwärtskante (engl. backedge). Wenn man im Zuge einer Tiefensuche eines Kontrollflussgraphen , die beim Knoten startet, ausgehend von einem Knoten entlang der Kante zu einem Knoten gelangt, der schon entdeckt worden ist, so nennt man die Kante Rückwärtskante.
Ein Kontrollflussgraph ist genau dann reduzibel, wenn er eine der folgenden drei (untereinander äquivalenten) Bedingungen erfüllt.
- Jede Tiefensuche findet dieselbe Menge an Rückwärtskanten.
- Sei eine Rückwärtskante. Dann dominiert den Knoten .
- enthält keinen Untergraphen der Form
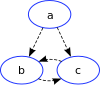 , wobei die eingezeichneten gestrichelten Kanten Pfade repräsentieren.
, wobei die eingezeichneten gestrichelten Kanten Pfade repräsentieren.
Nicht reduzierbare Kontrollflussgraphen nennt man irreduzierbar.
Die Unterscheidung in reduzierbare und irreduzierbare Kontrollflussgraphen ist in der Informatik insofern von Interesse, als für reduzierbare Kontrollflussgraphen im Allgemeinen effizientere Algorithmen existieren.
Bibliographie
[Bearbeiten | Quelltext bearbeiten]- ↑ Frances E. Allen: Control flow analysis. In: SIGPLAN Notices. Band 5, Nr. 7, Juli 1970, S. 1–19.
- ↑ Matthew S. Hecht, Jeffrey D. Ullman: Flow Graph Reducibility. In: STOC. 1972, S. 238–250.
- ↑ Matthew S. Hecht, Jeffrey D. Ullman: Characterizations of Reducible Flow Graphs. In: Journal of the ACM. Band 21, Nr. 3, Juli 1974, S. 367–375.






