Schraubfläche
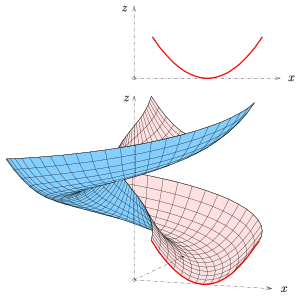
Eine Schraubfläche ist in der Geometrie eine Fläche, die durch eine Verschraubung einer Kurve im euklidischen Raum entsteht. Liegt die Kurve in einer Ebene mit der Schraubachse, so nennt man sie Meridian. Die einfachsten Schraubflächen sind die Wendelflächen. Sie entstehen durch Verschraubung einer die Schraubachse senkrecht schneidenden Gerade. Wichtige Typen von Schraubflächen sind die
- Regelschraubflächen oder Strahlschraubflächen. Sie entstehen durch die Verschraubung einer Gerade und sind deshalb Regelflächen.
- Kreisschraubflächen oder zyklische Schraubflächen. Sie entstehen durch die Verschraubung eines Kreises.
Wendelflächen spielen in der Mathematik eine wichtige Rolle (siehe Minimalfläche). In der Technik spielen beide Typen eine Rolle (Treppen, Rutsche, Schrauben, Rohre).
Bei technischen Anwendungen sind auch andere Profile (Parabel, Trapez, …) von Bedeutung.
Analytische Beschreibung
[Bearbeiten | Quelltext bearbeiten]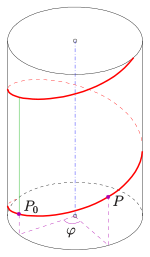
grün: Ganghöhe,
blau: Schraubachse
Verschraubung eines Punktes
[Bearbeiten | Quelltext bearbeiten]Die Verschraubung eines Punktes kann man sich als eine Überlagerung einer Drehung und einer Verschiebung in Richtung der Drehachse proportional zum Drehwinkel vorstellen.
Die Verschraubung des Punktes um die z-Achse lässt sich durch
beschreiben. Dabei ist der Schraubparameter, der Winkel , im Bogenmaß gemessen, der Schraubwinkel und die Ganghöhe (grün). Die Bahn des Punktes ist eine Schraublinie (rot). Sie liegt auf einem geraden Zylinder, dessen Radius gleich dem Abstand des Punktes von der Schraubachse ist.
Falls ist, nennt man die entstehende Schraublinie rechtsgängig andernfalls linksgängig. (Für würde eine Rotation um die z-Achse entstehen).
Verschraubung einer Kurve
[Bearbeiten | Quelltext bearbeiten]Die Verschraubung der Kurve
liefert die Schraubfläche mit der Parameterdarstellung
Die Flächenkurven sind Schraublinien.
Die Flächenkurven sind Kopien der gegebenen Kurve.
Regelschraubflächen
[Bearbeiten | Quelltext bearbeiten]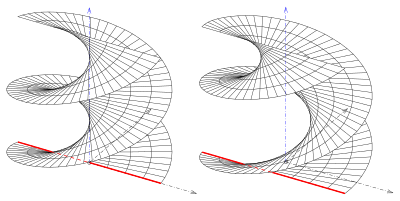
Typen
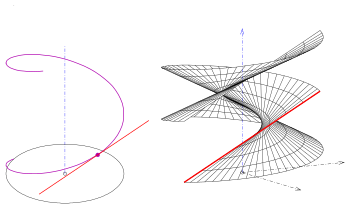
[Bearbeiten | Quelltext bearbeiten]Ist die gegebene Kurve eine Gerade, so entsteht eine Regelschraubfläche. Dabei sind 4 Fälle zu unterscheiden:
- (1) Die Gerade schneidet die Schraubachse senkrecht. Es entsteht eine Wendelfläche (geschlossene gerade Regelschraubfläche).
- (2) Die Gerade schneidet die Achse, aber nicht senkrecht. Es entsteht eine schiefe geschlossene oder scharfgängige Regelschraubfläche.
Ist die Gerade windschief zur Schraubachse, entsteht eine offene Regelschraubfläche. Im Gegensatz zur geschlossenen Regelschraubfläche gehört in diesem Fall die Schraubachse nicht zur Fläche. Die Flächenpunkte haben mindestens den Abstand der Ausgangsgerade von der Achse.
- (3) Ist die Gerade windschief in einer zur Achse senkrechten Ebene enthalten, entsteht eine gerade offene Regelschraubfläche oder kurz offene Wendelfläche.
- (4) Ist die Gerade windschief und nicht in einer zur Achse senkrechten Ebene enthalten, entsteht eine schiefe offene Regelschraubfläche.
Schiefe Regelschraubflächen durchdringen sich (s. Bild), gerade (Wendelflächen) nicht.
Ein interessanter Sonderfall der schiefen offenen Regelschraubflächen liegt vor, wenn die verschraubte Gerade den Abstand von der Schraubachse und gegenüber der x-y-Ebene den Neigungswinkel mit besitzt. In diesem Fall lässt sich die Fläche als Torse auffassen. Sie ist die Tangentenfläche der Schraublinie (Leitkurve) , d. h., sie ist die Vereinigung aller Tangenten der Schraublinie. Als Torse ist diese Regelschraubfläche abwickelbar.
Bemerkung:
- Die Wendelflächen sind Catalansche Flächen. Die geschlossene Wendelfläche ist sogar ein gerades Konoid.
- Strahlschraubflächen sind keine algebraische Flächen, d. h., sie lassen sich nicht mit einer algebraischen Gleichung implizit beschreiben. Plausibel wird dies durch die Tatsache, dass es immer eine zur Schraubachse parallele Gerade gibt, die die Fläche in unendlich vielen Punkten schneidet, obwohl sie nicht der Fläche angehört.
Über geschlossene Regelschraubflächen
[Bearbeiten | Quelltext bearbeiten]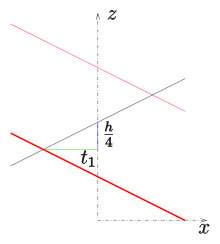
Bei einer geschlossenen Regelschraubfläche schneidet die Gerade die Schraubachse. Beschreibt man die zu verschraubende Gerade durch so ergibt sich die Parameterdarstellung
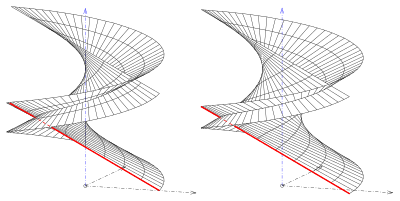
Falls (geschlossene Wendelfläche) ist, durchdringt sich die Fläche nicht selbst.
Falls (schiefe geschlossene Regelschraubfläche) ist, sind die Flächenkurven
- mit Selbstdurchdringungskurven (Doppelkurven).
Dies sind unendlich viele Schraublinien. Je kleiner ist, desto weiter liegen die Doppelkurven auseinander.
Über die Schraubtorse
[Bearbeiten | Quelltext bearbeiten]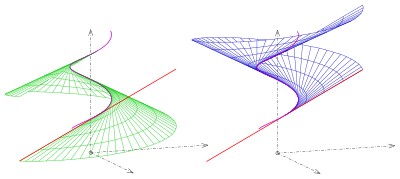
Geht man von der Schraublinie
- aus, so besitzt die zugehörige Schraubtorse die Parameterdarstellung:
Für die Flächennormale ergibt sich
Für ist der Normalenvektor der Nullvektor, d. h., die Ausgangskurve (Schraublinie) besteht aus den singulären Punkten der Fläche. Die Ausgangskurve heißt Gratlinie der Schraubtorse. Die Gratlinie trennt die Fläche in zwei reguläre Teilflächen (siehe Bild).
Kreisschraubflächen
[Bearbeiten | Quelltext bearbeiten]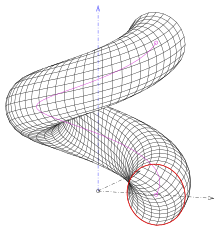
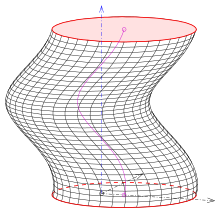
Unter den Kreisschraubflächen gibt es 3 interessante Typen:
- (1) Ist der Kreis ein Meridian und schneidet nicht die Schraubachse, so entsteht eine Meridiankreisschraubfläche (s. Bild).
- (2) Ist die Kreisebene senkrecht zur Schraublinie des Kreis-Mittelpunktes, so entsteht eine Rohrfläche. Eine Rohrfläche ist auch die Einhüllende von Kugeln mit dem gleichen Radius, deren Mittelpunkte die verschraubten Kreismittelpunkte sind.
- (3) Ist der Kreis horizontal (in einer zur Schraubachse senkrechten Ebene) und umfasst die Schraubachse, so entsteht eine säulenförmige gerade Kreisschraubfläche (s. Bild). Sie wurde bei Barock-Säulen gerne verwandt.
-
Uni-Mannheim Neubau Rettungsleiter
-
Rutsche Salinarium
-
Kanzelaltar (1688), St. Pankratius, Neuenfelde, Deutschland
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Weblinks
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Ulrich Graf, Martin Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, S. 218.
- Karl Strubecker: Vorlesungen über Darstellende Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967, S. 286.




























