Baum primitiver pythagoreischer Tripel

Berggrens Baum der primitiven pythagoreischen Tripel

In der Mathematik ist der Baum primitiver pythagoreischer Tripel ein Datenbaum, in dem jeder Knoten zu drei nachfolgenden Knoten verzweigt, wobei die unendliche Menge aller Knoten alle (und nur die) primitiven pythagoreischen Tripel ohne Duplikate ergibt.

Ein pythagoreisches Tripel ist eine Menge von drei positiven ganzen Zahlen a, b und c mit der Eigenschaft, dass sie jeweils die Seitenlängen eines rechtwinkligen Dreiecks sein können, wodurch die Gleichung $a^{2}+b^{2}=c^{2}$ erfüllt wird. Das Tripel gilt genau dann als primitiv, wenn der größte gemeinsame Teiler von a, b und c eins ist. Primitive pythagoreische Tripel (a, b, c) sind sogar paarweise teilerfremd. Die Menge aller primitiven pythagoreischen Tripel hat auf natürliche Weise die Struktur eines Wurzelbaums, insbesondere eines ternären Baums. Dies wurde erstmals 1934 von B. Berggren entdeckt.

F. J. M. Barning zeigte Folgendes: Wenn eine der folgenden Matrizen

${\begin{array}{lcr}A={\begin{bmatrix}1&-2&2\\2&-1&2\\2&-2&3\end{bmatrix}}&B={\begin{bmatrix}1&2&2\\2&1&2\\2&2&3\end{bmatrix}}&C={\begin{bmatrix}-1&2&2\\-2&1&2\\-2&2&3\end{bmatrix}}\end{array}}$

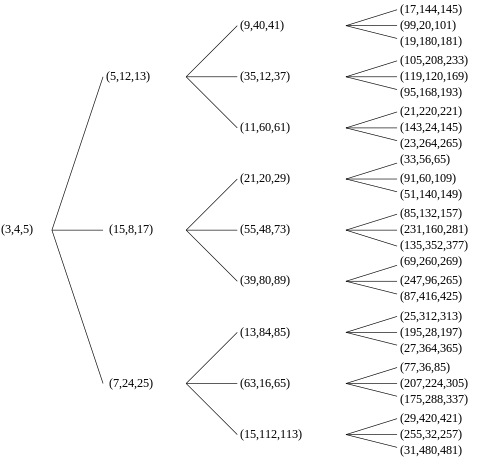
rechts mit einem Spaltenvektor, dessen Komponenten ein pythagoreisches Tripel bilden, multipliziert wird, dann ist das Ergebnis ein weiterer Spaltenvektor, dessen Komponenten ein anderes pythagoreisches Tripel bilden. Wenn das anfängliche Tripel primitiv ist, ist auch das so errechnete Tripel primitiv. Somit hat jedes primitive pythagoreische Tripel drei „Kinder“. Alle primitiven pythagoreischen Tripel stammen auf diese Weise vom Tripel (3, 4, 5) ab, und kein primitives Tripel erscheint mehr als einmal. Das Ergebnis kann grafisch als unendlicher ternärer Baum mit (3, 4, 5) als Wurzelknoten dargestellt werden (siehe klassischer Baum rechts). Dieser Baum erschien auch in Papieren von A. Hall im Jahr 1970 und A. R. Kanga im Jahr 1990. Im Jahr 2008 zeigte V. E. Firstov allgemein, dass nur drei solcher Bäume existieren und explizit einen Baum ähnlich dem von Berggren ergeben, jedoch beginnend mit dem Anfangsknoten (4, 3, 5).

Beweise

Vorhandensein ausschließlich primitiver pythagoreischer Tripel

Es kann durch vollständige Induktion gezeigt werden, dass der Baum primitive pythagoreische Tripel und nichts anderes enthält, indem gezeigt wird, dass ausgehend von einem primitiven pythagoreischen Tripel (wie es am Anfangsknoten mit (3, 4, 5) vorhanden ist), jedes erzeugte Tripel sowohl pythagoreisch als auch primitiv ist.

Erhaltung der pythagoreischen Eigenschaft

Wenn eine der obigen Matrizen, sagen wir A, auf ein Tripel (a, b, c)^T mit der pythagoreischen Eigenschaft $a^{2}+b^{2}=c^{2}$ angewendet wird, um ein neues Tripel zu erhalten (d, e, f)^T = A (a, b, c)^T, so ist dieses neue Tripel auch pythagoreisch. Dies kann gezeigt werden, indem jedes von d, e und f als die Summe der drei Terme mit a, b und c geschrieben wird, dann jedes von ihnen quadrieren und ersetzen von $c^{2}=a^{2}+b^{2}$ um $f^{2}=d^{2}+e^{2}$ zu erhalten. Dies gilt sowohl für B und C als auch für A.

Erhaltung der Primitivität

Die Matrizen A,B und C sind alle unimodular – das heißt, sie haben nur ganzzahlige Einträge und ihre Determinanten sind ±1. Somit sind ihre Inversen auch unimodular und haben insbesondere nur ganzzahlige Einträge. Wenn also eine von ihnen, zum Beispiel A, auf ein primitives pythagoreisches Tripel (a, b, c)^T angewendet wird, erhält man ein weiteres Tripel (d, e, f)^T. Wir haben (d, e, f)^T = A (a, b, c)^T und damit (a, b, c)^T = A⁻¹ (d, e, f)^T. Wenn irgendeine Primzahl zwei von (und damit alle drei von) d, e und f teilen würde, dann würde diese Primzahl durch diese letzte Gleichung auch jeden von a, b und c teilen. Wenn also a, b und c tatsächlich paarweise teilerfremd sind, dann müssen d, e und f auch paarweise teilerfremd sein. Dies gilt sowohl für B und C als auch für A.

Anwesenheit jedes primitiven pythagoreischen Tripels genau einmal

Um zu zeigen, dass der Baum jedes primitive pythagoreische Tripel enthält, jedoch nicht mehr als einmal, genügt es zu zeigen, dass es für ein solches Tripel genau einen Pfad zurück durch den Baum zum Startknoten (3, 4, 5) gibt. Dies kann man sehen, indem nacheinander jede der unimodularen inversen Matrizen A⁻¹, B⁻¹ und C⁻¹ auf ein beliebiges primitives pythagoreisches Tripel (d, e, f) angewendet wird, wobei zu beachten ist, dass durch die obige Argumentation die Primitivität und die pythagoreische Eigenschaft erhalten bleiben, und unter Hinweis darauf, dass für jedes Tripel, das größer als (3, 4, 5) ist, genau eine der inversen Übergangsmatrizen ein neues Tripel mit allen positiven Einträgen (und einer kleineren Hypotenuse) ergibt. Durch Induktion führt dieses neue gültige Tripel selbst zu genau einem kleineren gültigen Tripel und so weiter. Durch die Endlichkeit der Anzahl immer kleinerer potentieller Hypotenusen wird schließlich (3, 4, 5) erreicht. Dies beweist, dass (d, e, f) tatsächlich im Baum vorkommt, da es von (3, 4, 5) durch Umkehren der Schritte erreicht werden kann; und es kommt eindeutig vor, weil es nur einen Pfad von (d, e, f) zu (3, 4, 5) gibt.

Eigenschaften

Die Transformation unter Verwendung der Matrix A, wenn sie wiederholt von (a, b, c) = (3, 4, 5) durchgeführt wird, bewahrt das Merkmal $b+1=c$; die Matrix B bewahrt $|a-b|=1$; und die Matrix C bewahrt die Beziehung $a+2=c$.

Eine geometrische Interpretation für diesen Baum beinhaltet die an jedem Knoten vorhandenen Ankreise. Die drei Kinder eines Elterndreiecks „erben“ ihren Inkreisradius vom Elterndreieck: Die Ankreisradien des Elternteils werden zu den Inkreisradien für die nächste Generation. Zum Beispiel hat das Elterndreieck (3, 4, 5) die Ankreisradien 2, 3 und 6. Dies sind genau die Inkreisradien der drei Kinder (5, 12, 13), (15, 8, 17) und (21, 20, 29).

Wird A oder C wiederholt auf ein pythagoreisches Tripel angewendet, dann kann die Dynamik von a, b und c als die Dynamik von x in folgender Gleichung ausgedrückt werden

$x_{n+3}-3x_{n+2}+3x_{n+1}-x_{n}=0$,

die strukturell den charakteristischen Polynomen der Matrizen A und C gleicht:

$\lambda ^{3}-3\lambda ^{2}+3\lambda -1=0$

Wird B wiederholt auf ein pythagoreisches Tripel angewendet, entspricht die Dynamik von a, b und c der Dynamik von x wie folgt

$x_{n+3}-5x_{n+2}-5x_{n+1}+x_{n}=0$,

was strukturell dem charakteristischen Polynom von B gleicht.

Darüber hinaus kann eine Unendlichkeit von Differenzengleichungen 3. Ordnung gefunden werden, indem die drei Matrizen beliebig oft in einer beliebigen Reihenfolge miteinander multipliziert werden. Zum Beispiel bewegt die Matrix D = CB einen Knoten im Baum um zwei Positionen (quer, dann runter) in einem einzigen Schritt. Das charakteristische Polynom von D liefert das Muster für die Dynamik 3. Ordnung von a, b oder c in dem durch D gebildeten Baum.

Alternative Methoden zum Generieren des Baums

Ein anderer Ansatz zur Dynamik dieses Baums beruht auf der Standardformel zur Erzeugung aller primitiven pythagoreischen Tripel:

$a=m^{2}-n^{2},$

$b=2mn,$

$c=m^{2}+n^{2},$

mit m > n > 0 und m und n teilerfremd und unterschiedlicher Parität. Paare (m, n) können iteriert werden, indem eine der folgenden Matrizen mit dem Vorgängerpaar als Spaltenvektor multipliziert wird.

${\begin{array}{lcr}{\begin{bmatrix}2&-1\\1&0\end{bmatrix}},&{\begin{bmatrix}2&1\\1&0\end{bmatrix}},&{\begin{bmatrix}1&2\\0&1\end{bmatrix}}.\end{array}}$

Jede der Multiplikationen bewahrt die obige Ungleichung, die Teilerfremdheit und die entgegengesetzte Parität. Der resultierende ternäre Baum – beginnend bei (2,1) – enthält jedes solche (m, n)-Paar genau einmal, und wenn es in (a, b, c) konvertiert wird, entsteht exakt der oben beschriebenen Baum.

Eine andere Möglichkeit – mit zwei zugrunde liegenden Parametern zum Generieren des Dreifachbaums – verwendet eine alternative Formel für alle primitiven Tripel:

$a=uv,$

$b={\frac {u^{2}-v^{2}}{2}},$

$c={\frac {u^{2}+v^{2}}{2}},$

mit u > v > 0 und u und v teilerfremd und beide ungerade. Paare (u, v) können iteriert werden, indem eine der obigen (2 × 2)-Matrizen mit dem Vorgängerpaar als Spaltenvektor multipliziert wird. Jede der Multiplikationen bewahrt die obige Ungleichung, die Teilerfremdheit und dass beide Terme ungerade sind. Wenn dieser Prozess bei (3, 1) begonnen wird, enthält der resultierende ternäre Baum jedes solche (u, v)-Paar genau einmal, und wenn es in (a, b, c) konvertiert wird, entsteht ebenso der oben beschriebenen Baum.

Ein anderer Baum

Prices Baum der primitiven pythagoreischen Tripel

Alternativ kann man auch drei andere Matrizen verwenden, die von Price gefunden wurden. Diese Matrizen A', B', C' lauten:

${\overset {{A}'}{\mathop {\left[{\begin{matrix}2&1&-1\\-2&2&2\\-2&1&3\end{matrix}}\right]} }}\left[{\begin{matrix}a\\b\\c\end{matrix}}\right]=\left[{\begin{matrix}a_{1}\\b_{1}\\c_{1}\end{matrix}}\right],\quad {\text{ }}{\overset {{B}'}{\mathop {\left[{\begin{matrix}2&1&1\\2&-2&2\\2&-1&3\end{matrix}}\right]} }}\left[{\begin{matrix}a\\b\\c\\\end{matrix}}\right]=\left[{\begin{matrix}a_{2}\\b_{2}\\c_{2}\end{matrix}}\right],\quad {\text{ }}{\overset {{C}'}{\mathop {\left[{\begin{matrix}2&-1&1\\2&2&2\\2&1&3\\\end{matrix}}\right]} }}\left[{\begin{matrix}a\\b\\c\\\end{matrix}}\right]=\left[{\begin{matrix}a_{3}\\b_{3}\\c_{3}\end{matrix}}\right]$

Ihre entsprechenden linearen Transformationen sind:

${\begin{aligned}&{\begin{matrix}+2a+b-c=a_{1}\quad &-2a+2b+2c=b_{1}\quad &-2a+b+3c=c_{1}&\quad \to \left[{\text{ }}a_{1},{\text{ }}b_{1},{\text{ }}c_{1}\right]\end{matrix}}\\&{\begin{matrix}+2a+b+c=a_{2}\quad &+2a-2b+2c=b_{2}\quad &+2a-b+3c=c_{2}&\quad \to \left[{\text{ }}a_{2},{\text{ }}b_{2},{\text{ }}c_{2}\right]\end{matrix}}\\&{\begin{matrix}+2a-b+c=a_{3}\quad &+2a+2b+2c=b_{3}\quad &+2a+b+3c=c_{3}&\quad \to \left[{\text{ }}a_{3},{\text{ }}b_{3},{\text{ }}c_{3}\right]\end{matrix}}\\&\end{aligned}}$

Die drei Kinder, die von jedem der beiden Sätze von Matrizen (Berggren und Price) erzeugt werden, sind nicht gleich, aber jeder Satz erzeugt separat alle primitiven Tripel. Wenn man beispielsweise (5, 12, 13) als Eltern-Tripel verwendet, erhält man zwei Sätze mit je drei Kindern:

${\begin{array}{ccc}&\left[5,12,13\right]&\\A&B&C\\\left[45,28,53\right]&\left[55,48,73\right]&\left[7,24,25\right]\end{array}}\quad \quad \quad \quad \quad \quad {\begin{array}{ccc}&\left[5,12,13\right]&\\A'&B'&C'\\\left[9,40,41\right]&\left[35,12,37\right]&\left[11,60,61\right]\end{array}}$