Nepersche Ungleichung
Die Nepersche Ungleichung (englisch Napier’s inequality) ist eine Ungleichung des mathematischen Teilgebiets der Analysis, die auf den schottischen Mathematiker John Napier (1550–1617) zurückgeht. Sie liefert elementare untere und obere Abschätzungen für den reellen natürlichen Logarithmus.[1]
Darstellung der Ungleichung[Bearbeiten | Quelltext bearbeiten]
Die Ungleichung lautet folgendermaßen:[1]
- Gegeben seien zwei reelle Zahlen und und es gelte .
- Dann bestehen die Ungleichungen
- (N) .
Herleitung der Neperschen Ungleichung mittels Differenzialrechnung[Bearbeiten | Quelltext bearbeiten]
Für die Steigungen der Tangenten , und der Sehne gilt:
- ,
woraus unmittelbar die Nepersche Ungleichung folgt. (siehe Figur 1)
Herleitung der Neperschen Ungleichung mittels Integralrechnung[Bearbeiten | Quelltext bearbeiten]
Aus
folgt nach elementaren Umformungen und Stammfunktionsbildung
- (N') .
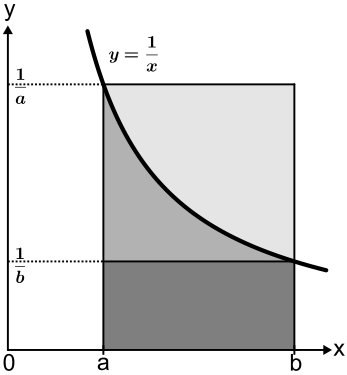
Also erhält man die Neperschen Ungleichung mittels Integralrechnung. Denn danach ist der mittlere Term von (N') nichts weiter als der Inhalt der Fläche unterhalb des Funktionsgraphs der reellen Kehrwertfunktion im Intervall . (siehe Figur 2)
Grafische Darstellungen der beiden Herleitungen[Bearbeiten | Quelltext bearbeiten]
Die beiden Herleitungen lassen sich durch grafische Veranschaulichungen unterstützen.[2][3]
-
Figur 1 zum Beweis der Napier-Ungleichung mittels Differenzialrechnung
-
Figur 2 zum Beweis der Napier-Ungleichung mittels Integralrechnung
Anwendung[Bearbeiten | Quelltext bearbeiten]
Eine nützliche Anwendung der Neperschen Ungleichung ergibt sich, wenn man darin sowie – für eine natürliche Zahl – noch setzt.
Dann nämlich ergibt sich wegen und
und weiter
und schließlich
- .
Durch Limesbildung erhält man dann
und es folgt aus Stetigkeitsgründen und durch Anwendung der Exponentialfunktion
- .
Verwandte Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Die Nepersche Ungleichung lässt sich erheblich verschärfen. Dies zeigt etwa die Ungleichung von Hermite-Hadamard, welche die Nepersche Ungleichung nach sich zieht. Denn berücksichtigt man hier die Tatsache, dass die Einschränkung der reellen Umkehrfunktion auf das Intervall der positiven Zahlen eine konvexe Funktion ist, so ergeben sich für sogleich die Abschätzungen
und damit
- .[4]
Für den Fall, dass insbesondere ist, hat man sogar die folgenden – und für diesen Fall besseren! – Abschätzungen:[5]
- .
Literatur[Bearbeiten | Quelltext bearbeiten]
- Claudi Alsina, Roger B. Nelsen: Math Made Visual: Creating Images for Understanding Mathematics (= Classroom Resource Materials Series). The Mathematical Association of America, Washington, DC 2006, ISBN 0-88385-746-4 (MR2216733).
- D. S. Mitrinović: Analytic Inequalities. In cooperation with P. M. Vasić (= Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete. Band 165). Springer Verlag, Berlin (u. a.) 1970, ISBN 3-540-62903-3 (MR0274686).
- Guido Walz: Lexikon der Mathematik, Band 4, zweite Auflage, Springer Spektrum, Berlin 2017, ISBN 978-3-662-53499-1, Seite 22
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Napier-Ungleichung Lexikon der Mathematik aus Spektrum der Wissenschaft, abgerufen am 25. Januar 2023
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b Claudi Alsina, Roger B. Nelsen: Math Made Visual: Creating Images for Understanding Mathematics. 2006, S. 16
- ↑ Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 149
- ↑ College Mathematics Journal, vol. 24, no. 2 (March 1993), S. 165
- ↑ Die vordere Ungleichung, wenn auch formuliert für die Kehrwerte, findet man in: D. S. Mitrinović: Analytic Inequalities. 1970, S. 273
- ↑ D. S. Mitrinović: Analytic Inequalities. 1970, S. 273–274










![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)











![{\displaystyle ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/103a5a305a61f6370460c3c4c6882164cd4e0ff4)



