Schachbrett-Paradoxon

Das Schachbrett-Paradoxon[1][2] oder Paradoxon von Loyd und Schlömilch[3] ist ein Scheinparadox, das auf einem geometrischen Trugschluss beruht. Hierbei wird ein Schachbrett beziehungsweise ein Quadrat mit einer Seitenlänge von 8 Längeneinheiten in vier Teile zerschnitten, die man anschließend zu einem Rechteck zusammensetzt. Dieses Rechteck besitzt eine Länge von 13 Längeneinheiten und eine Breite von 5 Längeneinheiten und damit eine Fläche von 65 Flächeneinheiten, was im Widerspruch zu der Tatsache steht, dass die Summe der Flächen der vier Teile (= Quadratfläche) lediglich 64 Flächeneinheiten beträgt. Dieser Widerspruch erklärt sich dadurch, dass die vier Teile, wenn sie zu dem Rechteck zusammengesetzt werden, nur scheinbar exakt zueinander passen und dieser Unterschied mit bloßem Auge kaum erkennbar ist. Das Scheinparadox ist nach dem amerikanischen Puzzle-Spezialisten Samuel Loyd (1841–1911) und dem deutschen Mathematiker Oskar Schlömilch (1832–1901) benannt.
Analyse des Scheinparadox[Bearbeiten | Quelltext bearbeiten]

Bei genauer Betrachtung fügen sich die vier Quadrat-Teile nicht nahtlos aneinander, stattdessen entsteht an der Diagonale des Rechtecks eine schmale Lücke in Form eines Parallelogramms, die für den Flächenzuwachs verantwortlich ist.
Dass es sich bei dem Viereck tatsächlich um ein Parallelogramm handelt, erkennt man daran, dass die gegenüberliegende Winkel gleich groß sind:[4]
Alternativ kann man die Parallelität der Seiten auch überprüfen, indem man das Rechteck in einem Koordinatensystem platziert und die Steigungen bzw. die vektorielle Darstellung der Seiten berechnet.
Ebenso kann man nutzen, dass das Rechteck (einschließlich des innenliegenden Vierecks ) offensichtlich drehsymmetrisch (-Drehung) beziehungsweise punktsymmetrisch zu seinem Diagonalenschnittpunkt ist, wodurch die entsprechenden Seiten parallel sind.
Es würde auch genügen zu erkennen, dass die Seiten und zueinander parallel und gleich lang sind (sie wurden lediglich parallel verschoben).
Als Seitenlängen und Diagonalen des Parallelogramms erhält man:
Mit der Formel von Heron lässt sich die Fläche des halben Parallelogramms () berechnen, hierbei ist der halbierte Umfang
und für die Fläche des gesamten Parallelogramms ergibt sich dann:
Die Parallelogrammlücke im Rechteck entspricht damit exakt dem Flächenzuwachs.
Verallgemeinerung[Bearbeiten | Quelltext bearbeiten]


die Dreiecke sind fast ähnlich

Betrachtet man die Längen der senkrecht aufeinander stehenden Strecken, die in der Zeichnung des Rechtecks im vorherigen Abschnitt auftreten, so erhält man 2, 3, 5, 8 und 13. Dies sind aufeinander folgende Fibonacci-Zahlen. Die Verwendung der Fibonacci-Zahlen liefert eine tieferliegende Erklärung, warum sich die gewählten Streckenlängen zur Zerlegung des Quadrats besonders gut für den geometrischen Trugschluss beziehungsweise die optische Täuschung eignen und warum der Flächenzuwachs genau eine Flächeneinheit beträgt. Zudem erhält man ein Verallgemeinerung des Paradoxon auf Quadrate, deren Seitenlänge einer Fibonacci-Zahl entspricht. So wie man das Quadrat der Seitenlänge 8 mit Hilfe der Streckenlängen 8, 5 und 3 zerlegt hat, kann man auch ein Quadrat der Seitenlänge mit Hilfe der Streckenlängen , und zerlegen (siehe Zeichnung).
Für Fibonacci-Zahlen gilt die Cassini-Identität:[5]
Anhand dieser sieht man sofort, dass der Flächenunterschied zwischen Quadrat und Rechteck immer eine Flächeneinheit betragen muss, insbesondere gilt für das ursprüngliche Schachbrett-Paradoxon mit :
Wenn ungerade ist, so ist das Rechteck nicht um eine Flächeneinheit größer, sondern kleiner. Dies liegt daran, dass sich in diesem Fall keine schmale Lücke an der Diagonalen bildet, sondern die Quadrat-Teile dort leicht überlappen.
Da das Verhältnis zweier aufeinander folgender Fibonacci-Zahlen sehr schnell gegen den goldenen Schnitt konvergiert, gilt:
Die vier Quadrat-Teile passen genau dann nahtlos aneinander, wenn das Parallelogramm zu einer Strecke entartet und damit mit der Rechteck-Diagonalen zusammenfällt. In diesem Fall gilt für die Winkel
- , , , ,
da es sich um Stufenwinkel an Parallelen handelt, zudem sind damit die Dreiecke , , und alle ähnlich zueinander. Aus der Gleichheit der Winkel folgt die Gleichheit der zugehörigen Tangens-Werte, die im Rechteck den Brüchen
- ,, und
entsprechen. Aufgrund der obigen Konvergenz gilt nun:
Damit sind die Tangens-Werte und die zugehörigen Winkel fast gleich, die Dreiecke fast ähnlich und die vier Quadrat-Teile passen scheinbar exakt zueinander. Daher eignen sich die Fibonacci-Zahlen besonders gut für die optische Täuschung.[5]
Es ist aber möglich, das Quadrat nach dem vorgegebenen Muster in vier Teile zu zerlegen, die sich exakt zu einem Rechteck der gleichen Fläche zusammensetzen lassen. Dies erreicht man, indem man für die Streckenlängen nicht die Fibonacci-Zahlen wählt, sondern sie direkt vom goldenen Schnitt ableitet (siehe Zeichnung). Man erhält dann für die Fläche des Rechtecks, das aus der Zerlegung eines Quadrats mit Seitenlänge entstanden ist,[5]
- ,
da eine Eigenschaft des goldenen Schnitts ist.
Geschichte[Bearbeiten | Quelltext bearbeiten]
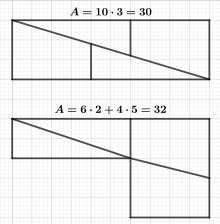
Das Paradox von Hooper ist ein geometrischer Trugschluss, der sich als ein Vorläufer des Schachbrett-Paradoxons ansehen lässt, da er dieselben Zerlegungsfiguren verwendet. Allerdings wird dort kein Quadrat zerlegt und die Zerlegung basiert auch noch nicht auf den Fibonacci-Zahlen. William Hooper veröffentlichte das nach ihm benannte Scheinparadox 1774 unter dem Titel The geometric money in seinem vierbändigen Werk Rational Recreations, zunächst noch mit einer fehlerhaften Zeichnung, die aber in der Ausgabe von 1783 korrigiert wurde. Das Paradox geht jedoch nicht auf Hooper selbst zurück, denn dessen Rational Recreations war im Wesentlichen eine Übersetzung der Nouvelles récréations physiques et mathétiques von Edmé Gilles Guyot (1706–1786). Dieses ebenfalls vierbändige Werk erschien 1769 in Frankreich und enthielt in seiner Erstausgabe dieselbe fehlerhafte Zeichnung.[1]
Die erste bekannte Veröffentlichung des eigentlichen Schach-Paradoxons stammt von Oskar Schlömilch und erschien 1868 als ein Beitrag mit dem Titel Ein geometrisches Paradoxon in der Zeitschrift für Mathematik und Physik. Victor Schlegel veröffentlichte 1879 in derselben Zeitschrift den Artikel Verallgemeinerung eines geometrischen Paradoxons, in dem der Bezug zu den Fibonacci-Zahlen hergestellt und zur Verallgemeinerung der Konstruktion benutzt wurde. Auch der Mathematiker und Autor Lewis Carroll beschäftigte sich mit dem Schachbrett-Paradoxon und untersuchte unabhängig von Schlegel eine Verallgemeinerung basierend auf den Fibonacci-Zahlen. Allerdings veröffentlichte er seine Erkenntnisse nicht, sondern seine undatierte und nicht vollständig ausgearbeitete Untersuchung wurde erst später in seinem Nachlass entdeckt. Der amerikanische Puzzle-Erfinder Samuel Loyd stellte das Schachbrett-Paradoxon nach eigenen Angaben erstmals auf dem internationalen Schachkongress 1858 vor, später war es Bestandteil des von seinem gleichnamigen Sohn herausgegebenen Werkes Sam Loyd's Cyclopedia of 5,000 Puzzles, Tricks and Conundrums (1914). In dieser ist auch die Zusammensetzung der vier Quadrat-Teile zu einer Figur mit 63 Flächeneinheiten enthalten, die Sam Loyds Sohn als seine Erfindung reklamierte. Allerdings findet sich diese Variante auch schon in dem Artikel Some postcard puzzles von Walter Dexter aus dem Jahre 1901.'[1][6]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Thomas Koshy: Fibonacci and Lucas Numbers with Applications. Wiley, 2001, ISBN 9781118031315, S. 100–108
- Martin Gardner: Mathematics, Magic and Mystery. Courier (Dover), 1956, ISBN 9780486203355, S. 129–155
- Franz Lemmermeyer: Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen. Springer 2014, ISBN 9783662452707, S. 95–96
- Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1996. ISBN 3-86025-404-9, S. 91–93
- Jean-Paul Delahaye: Au pays des paradoxes. Humensis, 2014, ISBN 9782842451363
- Greg N. Frederickson: Dissections: Plane and Fancy. Cambridge University Press, 2003, ISBN 9780521525824, Kapitel 23, S. 268–277 insbesondere S. 271–274 (Online-Update zu Kapitel 23)
- Miodrag Petkovic: Famous Puzzles of Great Mathematicians. AMS, 2009, ISBN 9780821848142, S. 14, 30–31
- A. F. Horadam: Fibonacci Sequences and a Geometrical Paradox. In: Mathematics Magazine, Band. 35, Nr. 1 (Jan., 1962), S. 1–11 (JSTOR)
- David Singmaster: Vanishing Area Puzzles. In: Recreational Mathematics Magazine, Nr. 1, März 2014
- Colin Foster: Slippery Slopes. In: Mathematics in School, Band 34, Nr. 3 (Mai, 2005), S. 33–34 (JSTOR)
- John F. Lamb Jr.: The Rug-cutting Puzzle. In: The Mathematics Teacher, Band 80, Nr. 1 (Januar 1987), S. 12–14 (JSTOR)
- Warren Weaver: Lewis Carroll and a Geometrical Paradox. In: The American Mathematical Monthly, Band 45, Nr. 4 (Apr., 1938), S. 234–236 (JSTOR)
- Oskar Schlömilch: Ein geometrisches Paradoxon. In: Zeitschrift für Mathematik und Physik, Band 13, 1868, S. 162
- Victor Schlegel: Verallgemeinerung eines geometrischen Paradoxons. In: Zeitschrift für Mathematik und Physik, Band 24, 1879, S. 123–128
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Jigsaw Paradox
- Eric W. Weisstein: DissectionFallacy. In: MathWorld (englisch).
- Schachbrett-Paradoxon
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b c Greg N. Frederickson: Dissections: Plane and Fancy. Cambridge University Press, 2003, ISBN 9780521525824, chapter 23, pp. 268–277 in particular pp. 271–274 (online update for chapter 23)
- ↑ Colin Foster: "Slippery Slopes". In: Mathematics in School, vol. 34, no. 3 (May, 2005), pp. 33–34 (JSTOR)
- ↑ Franz Lemmermeyer: Mathematik à la Carte: Elementargeometrie an Quadratwurzeln mit einigen geschichtlichen Bemerkungen. Springer 2014, ISBN 9783662452707, pp. 95–96 (German)
- ↑ Thomas Koshy: Fibonacci and Lucas Numbers with Applications. Wiley, 2001, ISBN 9781118031315, pp. 74, 100–108
- ↑ a b c Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1996. ISBN 3-86025-404-9, S. 91–93
- ↑ Martin Gardner: Mathematics, Magic and Mystery. Courier (Dover), 1956, ISBN 9780486203355, pp. 129–155








































