Seminumerischer Algorithmus
Seminumerische Algorithmen sind eine Kombination aus numerischen und analytischen oder algebraischen Verfahren in der Programmierung. Seminumerische Algorithmen sind meist gegenüber rein numerischen Verfahren genauer, erfordern jedoch oft einen höheren Implementierungsaufwand, da Vorwissen über die numerischen Zusammenhänge in Bezug auf spezialisierte Anwendungen oder Anforderungen eingearbeitet wird, anstelle allgemeine Verfahren zu nutzen.
Weit verbreitetes Anwendungsgebiet seminumerischer Implementierungen sind z. B. auch Computeralgebrasysteme, da mit ihnen auf elegante Weise numerische wie auch algebraische Verfahren kombiniert werden können.
Die Problematik der numerischen Berechnung aufeinanderfolgender kontinuierlich bis unstetig wirkende Übertragungssysteme in Verbindung mit logischen Entscheidungsfunktionen hat es in der Systemtheorie, der Steuerungstechnik und Regelungstechnik schon immer gegeben.
Es geht um zu berechnende mathematische Modelle von zusammenhängenden Übertragungssystemen, die zum Teil mit Differenzialgleichungen beschrieben werden können und um solche, die algebraisch oder mit logischen Anweisungen definiert werden müssen.
In der deutschsprachlichen Fachliteratur ist der Begriff der „Seminumerischen Algorithmen“ spärlich behandelt. In den Medien sind Abhandlungen über sehr spezielle Anwendungen veröffentlicht, die nur von „Experten“ verstanden werden können.
Dieser Artikel behandelt eine Konfiguration verschiedenartiger zusammenhängender dynamischer und statischer Übertragungssysteme, die numerisch berechnet werden sollen.
Ein typisches Praxisbeispiel eines seminumerischen Gesamtmodells mit einem Totzeitsystem und mehreren in Reihe liegenden Verzögerungsgliedern (PT1-Gliedern) erklärt die Zusammenhänge.
Grundlagen seminumerischer Algorithmen[Bearbeiten | Quelltext bearbeiten]
Eine gewöhnliche Differenzialgleichung (DGL) kann das Verhalten eines dynamischen Systems vollständig beschreiben. Nicht alle DGL-en sind auf konventionellem Wege einfach zu lösen. Abhilfe bieten die numerischen Verfahren, welche anstelle der kontinuierlichen Funktion der Systemausgangsgröße eine diskrete Lösung in Form von nummerierten Folgegliedern (Stützstellen) darstellen.
Die numerische Behandlung verschiedenster Übertragungssysteme stellt sich als tabellarisch geordnete Funktionen in Form einer gewählten endlichen Anzahl von nummerierten Folgengliedern dar. Meist interessiert die Systemsprungantwort der Ausgangsgröße y(t) des Gesamtsystems, wobei die verschiedenen Einzelsysteme sich auf die gemeinsame Nummerierung der diskreten unabhängigen Variable bzw. beziehen.
Die lineare Systemeigenschaft existiert in der Praxis häufig nicht, da viele zusammenwirkende Systeme z. B. in der Regelungs- und Steuerungstechnik bei Ventilkennlinien, Stellgrößenbegrenzungen oder Schaltvorgängen keine Linearität aufweisen. Ein Totzeitsystem ist wohl ein lineares System, es kann aber nicht durch eine DGL beschrieben werden. Für nichtlineare statische Systeme, die sich nicht durch Gleichungen beschreiben lassen, gelten Tabellenwerte, die sich mit anderen Systemen auf gleiche nummerierte Folgeglieder beziehen.
Für die Berechnung eines technischen Problems können die einzelnen Lösungsschritte wie folgt aussehen:
- Klärung des physikalischen Problems,
- Mathematische Einzelmodelle festlegen,
- Numerische Beschreibung der einzelnen Übertragungsmodelle,
- Numerisches Verfahren festlegen: Einschrittverfahren, Mehrschrittverfahren, und andere,
- Algorithmen für gemischte Systeme festlegen: (Algorithmen sind Anweisungen, wie und in welcher Reihenfolge ein (mathematisches) Problem zu lösen ist).
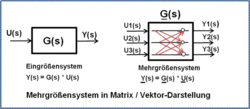
Definition Systembegriff[Bearbeiten | Quelltext bearbeiten]
- System: Aus mehreren Teilen zusammengesetztes Ganzes.
- Systemtheorie: Analyse von Strukturen, Dynamik und Funktionen. Abstrakte mathematisch Modelle mit Ein- und Ausgangssignalen beschreiben in der Systemtheorie das Systemverhalten verschiedenartigster dynamischer Systeme bei gegebenen Anfangszuständen völlig unabhängig von technologischen Details.[1]
- Systemeigenschaften: Eigenschaften, die für das System charakteristisch sind.
- Systemstruktur: Gesamtheit der Elemente eines Systems.
- Dynamisches System: Es ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht. Die Wirkung des Eingangssignals mit dem Systemverhalten und dem Systemzustand kann sich auf das Systemausgangssignal überlagern.
- Übertragungssystem: System mit mindestens einem oder mehreren Signaleingängen und einem oder mehreren Signalausgängen. Es kann sich zeitabhängig oder zeitunabhängig verhalten.
- Übertragungsfunktion: Laplace-transformierte lineare Differenzialgleichung, deren Ableitungen durch die unabhängige Variable s ersetzt wird.
- Statisches System (signaltechnisch): Jedes Ausgangssignal ist ohne Zeitverhalten unmittelbar vom Eingangssignal abhängig.
Numerische Verfahren[Bearbeiten | Quelltext bearbeiten]

Differenzengleichungen als einfachstes Verfahren der Numerik werden zur numerischen Berechnung in vielen wissenschaftlichen Disziplinen – wie Wirtschaft, Medizin, Technik, Elektrotechnik, Regelungstechnik, Kybernetik, Informatik, Akustik und andere – eingesetzt. Sie gehören zu den Einschrittverfahren.
Eine Differenzengleichung steht in enger Beziehung zu einer DGL. Die Differenzengleichung einer Verzögerungsfunktion einfacher und höherer Ordnung entsteht z. B., wenn der Differenzialquotient einer zu berechnenden DGL durch einen Differenzenquotient ausgetauscht wird. Durch diesen Vorgang entsteht automatisch das rekursive Verhalten der Differenzengleichung, bei der sich je nach Ordnung jedes aktuelle Folgeglied sich auf ein oder mehrere zurückliegende Folgeglieder bezieht.
Eine Differenzengleichungen höherer Ordnung verknüpft die Werte der Ausgangsfolgen entsprechend der Ordnung an zwei, drei oder mehreren zurückliegenden Zeitpunkten:
- Rekursion: .
Die Zahl der Wertefolgen bestimmt die Schrittweite und die Endgröße der unabhängigen Variable bei zeitabhängigen Systemen .
- ist der Darstellungszeitraum, Schrittweite.
Neben dem einfachen numerischen Verfahren mit Differenzengleichungen (Einschrittverfahren) stehen auch andere aufwendigere Verfahren (z. B. Mehrschrittverfahren) zur besseren Approximation an den analytischen Verlauf einer Funktion zur Verfügung. Dazu gehören z. B. das Trapezflächenverfahrens (Heun-Verfahren), Runge-Kutta-Verfahren, das Mehrschrittverfahren (Adams-Bashforth-Verfahren) und andere. Grund der aufwendigen Approximationsverfahren ist die erzielbare höhere Genauigkeit und damit erhebliche Reduzierung der Anzahl der Folgeglieder.[2]
- Bei in Reihe liegenden Übertragungssystemen ist die Ausgangsgröße die Eingangsgröße des nachfolgenden Systems. Es handelt sich dabei um eine Multiplikation der Einzelsysteme.
- Bei parallelwirkenden Übertragungssystemen werden die Ausgangsgrößen gleicher Folgeglieder addiert.[3]
- Die numerische Berechnung dynamischer und statischer Systeme kann mit jeder Programmiersprache durchgeführt werden.
Differenzengleichungen für dynamische Übertragungssysteme[Bearbeiten | Quelltext bearbeiten]
Dynamische Systeme werden mit DGL-en beschrieben. Werden die Differentialquotienten durch Differenzenquotienten ersetzt, entsteht eine Differenzengleichung, die leicht gelöst werden kann.
Unterschieden wird die Entstehungsweise der Differenzengleichungen durch den Vorwärts- und Rückwärts-Differenzenquotienten, die beide je nach Anwendung Vorteile haben. Differenzengleichungen nach der Rückwärtsdifferenz berechnen Folgewerte um eine Folge früher.
Die Differenzengleichungen der Methode Rückwärts-Differenz berechnen die Modelle der dynamischen Übertragungsglieder bei Reihenstruktur und dem Anfangswert immer je nach Größe der Schrittweite immer einen kleinen Wert , der bei kleiner Schrittweite vernachlässigbar ist.

Sprungantwort des PT1-Gliedes
Die Differenzengleichungen der Methode Vorwärts-Differenz berechnen die Modelle der dynamischen Übertragungsglieder bei Reihenstruktur und dem Anfangswert immer . Dies führt z. B. bei 4 hintereinander geschalteten Verzögerungsgliedern dazu, dass bei 4 Systemen das 4. System nach 4 Folgen immer noch für einen Wert von aufweist, was nachteilig ist.
Die Folgebezeichnungen der Systemausgangsgrößen , , sind relative Begriffe der Nummerierung. Sie haben erst eine absolute Bedeutung, wenn die Folge des ersten Folgegliedes der Folge der Differenzengleichung mit der Ausgangsgröße zugeordnet wird.
Differenzengleichung nach der Vorwärts-Differenz:
Für ist der 1. Folgewert ein Anfangswert. Die nächste Folge ist der 1. berechnete Wert der Ausgangsgröße .
Differenzengleichung nach der Rückwärts-Differenz:
Für berechnen die Differenzengleichungen für immer je nach Größe der Schrittweite einen kleinen Wert .
Dynamische Systeme werden mit DGL-en oder Übertragungsfunktionen exakt beschrieben. Die analytische Lösung einer DGL bezieht sich auf eine unendlich hohe Auflösung, die mit einer numerischen Lösung nicht erreicht werden kann.
Die numerische Lösung bei dynamischen Systemen ist immer eine Annäherung an die analytische Funktion. Mit kleiner werdender Schrittweite steigt linear die Genauigkeit der berechneten Folgeglieder und damit die Zahl der Folgeglieder. Zur Erzielung einer großen Genauigkeit der Folgeglieder kann die Zahl der Folgeglieder nicht beliebig hoch betrieben werden, weil sich je nach Rechengenauigkeit des Computers unvermeidbare Rundungsfehler zu jedem Folgeglied aufaddieren können.
Dynamische Übertragungssysteme als Übertragungsfunktionen G(s) 1. und höherer Ordnung lassen sich mit sogenannten Laplace-Transformationstafeln lösen. Bereits die Lösung von Übertragungsfunktionen 2. Ordnung erfordern gute Kenntnisse mit e-Funktionen und trigonometrischen Funktionen.
Exponentielles und arithmetisches Folgeverhalten numerischer Berechnungen[Bearbeiten | Quelltext bearbeiten]
Das rekursive Verhalten eines dynamischen Systems bestimmter Ordnung, d. h. der Bezug einer zu berechnenden Wertefolge auf eine zurückliegende Folge, ist nicht für alle dynamischen Systeme gleich. Die Folgen unterscheiden sich bei Übertragungssystemen wie folgt:
- Bei der arithmetischen Folge wächst oder fällt jedes Folgeglied um einen festen Betrag. (Beispiel: Sparschwein)
- Bei der exponentiellen Folge wächst oder fällt jedes Folgeglied um einen relativen Anteil. (Beispiel: Verzögerungssysteme, Zinseszins)
Exponentielle Folge[Bearbeiten | Quelltext bearbeiten]
Für alle Formen von dynamischen Verzögerungssystemen beliebiger Ordnung gilt die diskrete exponentielle Folge. Nur das Integrationsglied (I-Glied) 1. O. bildet eine Ausnahme. Die Berechnung dieser Gruppe der Verzögerungssysteme bedeutet immer nur eine Annäherung an die analytische Funktion.
Übertragungssysteme, die nicht mit DGL-en beschrieben werden, aber zeitabhängig sind, wie die bekannten Aufgabenstellungen, z. B. „Zinseszins“, „Bevölkerungswachstum“, „Flüssigkeitszufluss -Abfluss in Behältern“ und andere. Hierbei gilt eine feste Auflösung der Zeit wie [s], [Std], [Jahre], deren Anzahl der Zeitfolgen durch die Aufgabenstellung festgelegt ist. Die Anzahl der Zeitfolgen bestimmt die Schrittweite . Diese Wertefolgen der Ausgangsgröße verhalten sich exponentiell.
Da zwischen diesen Wertefolgen keine höheren Auflösungen existieren, sind diese Berechnungen exakt genau.
Typische exponentielle Form der Differenzengleichung:
Arithmetische Folge[Bearbeiten | Quelltext bearbeiten]
Das Sammeln von Ereignissen entspricht einer arithmetischen Folge, z. B. das Sparschwein.
Das zu den verzögernden dynamischen Übertragungsgliedern gehörende Integrationsglied (I-Glied) verhält sich proportional der diskreten Zeitfolge. Dieses Systemverhalten entspricht der arithmetischen Folge (keine Rekursionsgleichung). Siehe nachfolgendes Berechnungsbeispiel der Bildung einer Differenzengleichung des I-Gliedes.
Typische arithmetische Form der Differenzengleichung:

Zeitverhalten für einen Eingangssprung
Beispiel der Darstellung einer Differenzengleichung eines Integrationsgliedes (I-Glied)[Bearbeiten | Quelltext bearbeiten]
Übertragungsfunktion des I-Gliedes:
Differenzialgleichung des I-Gliedes:
Mittels der inversen Laplace-Transformation entsteht die DGL aus der Übertragungsfunktion.[4]
- .
Der Vorwärts-Differenzenquotient lautet:
Die Differenzengleichung nach dem Vorwärts-Differenzenquotienten lautet:
Die Differenzengleichung wird nach freigestellt: [5]
Das Verhalten des I-Gliedes für einen Eingangssprung über alle Folgen ist linear und nicht rekursiv. Es handelt sich hier um eine Werte-Zunahme von arithmetischen Folgen, d. h. die Differenz zweier aufeinander liegenden Folgen ist immer konstant.

Numerische Berechnung dynamischer Systeme mit Differenzialgleichungen zweiter und höherer Ordnung[Bearbeiten | Quelltext bearbeiten]
Folgende Verfahren zur Lösung von dynamischen Systemen mit konjugiert komplexen Polen sind bekannt:
- Lösung einer DGL 2. O. mit einem Modellregelkreis
- Lösung einer DGL höherer Ordnung mit Differenzenquotienten 2. Ordnung
- Lösung einer DGL höherer Ordnung mit Zustandsvariablen
- Sie lassen sich auch leicht nach dem den Signalflussplan der Regelungsnormalform des Zustandsraumes lösen.
Anmerkung: Die beiden Graphen sind optisch deckungsgleich, wenn an Stelle der Schrittweite die Schrittweite gewählt wird.
siehe auch Artikel Differenzengleichung (Differenzenverfahren).
Definition wichtiger seminumerischer Einzelsysteme[Bearbeiten | Quelltext bearbeiten]
Die tabellarische Verbindung der verschiedenen Systeme untereinander sind die diskreten Folgen (Stützstellen). Die Ausgangsgrößen eines Einzelsystems sind die Eingangsgrößen des nachfolgenden Systems.
Bei hintereinander liegenden dynamischen und statischen Übertragungsgliedern startet jedes System bei der Folge und mit der zugehörigen numerischen Gleichung.
In der Technik häufig auftretender Verbund linearer und nichtlinearer Systeme[Bearbeiten | Quelltext bearbeiten]
Dynamisches System
DifferenzialgleichungBegrenzungseffekte
SignalsprüngeNichtlineares
System TabelleSystemtotzeit
(Lineares System)Beispiel: DGL 1. O. des PT1-Gliedes IF-THEN-ELSE-
AnweisungDiskrete Zahlenwerte =INDEX-Anweisung der
Tabellenkalkulation
=INDEX(D1:D1000;1000-Tt / h)Differenzengleichung der Vorw.-Differenz Beispiel: Sprung, Rücksprung
Anweisung: =WENN(A1000<8;1;0).
:=WENN A1000<8; DANN 1; SONST 0Beispiel:
Wertefolgen:
Zahlen 0;0;0;2;5;8;11;...Beispiel Modell:
Nachbildung PT1-Glied 5. O.
ZeitkonstanteDifferenzengleichung der Rückw.-Differenz Beispiel Modell:
Allpassglied 3. O.
Gewöhnliche Differenzialgleichungen (Grundlagen)[Bearbeiten | Quelltext bearbeiten]
- Gewöhnlich bedeutet, die gesuchte Funktion hängt nur von einer Variablen ab. Die DGL enthält mindestens eine Ableitung von der gesuchten Funktion.
- Lineare Differenzialgleichung: y(x) und Ableitungen davon dürfen nur in der 1. Potenz vorkommen und keine Winkelfunktionen enthalten.
- Nichtlineare Differenzialgleichung: Die gesuchte Funktion und deren Ableitungen enthalten Potenzen höherer Ordnung oder Winkelfunktionen.
Diese DGL-en können je nach Ordnung leicht über Differenzengleichungen numerisch gelöst werden.
Übertragungsfunktion eines dynamischen Systems (Grundlagen)[Bearbeiten | Quelltext bearbeiten]
Eine große Vereinfachung der Berechnung der Systeme ergibt sich dann, wenn die Lösung der Differentialgleichung nicht im Zeitbereich, sondern im Bildbereich (s-Bereich) mittels Laplace-Transformation vorgenommen wird. Die Systemberechnung bezieht sich dann auf einfache algebraische Operationen. Voraussetzung ist, dass es sich bei dem System um ein LZI-System handelt und die Anfangsbedingungen Null sind.[6]
Vorgegebene Übertragungsfunktionen können nach der inversen Laplace-Transformation in den ursprünglichen Zustand der DGL-en zurückgesetzt werden. Für die numerische Berechnung dynamischer Systeme werden Systembeschreibungen in Form von DGL-en benötigt.
Definition der Totzeit Tt[Bearbeiten | Quelltext bearbeiten]
Eine Besonderheit ist das Totzeitsystem, dass nicht durch eine DGL beschrieben werden kann. Die numerische Berechnung bezieht sich auf eine Verschiebung der diskreten Folgen gegenüber einer Tabellenspalte z. B. der Systemeingangsgröße um Wertefolgen. Die INDEX-Anweisung der Tabellenkalkulation macht das automatisch und bezieht sich auf die zurückliegende Spalte der Eingangsgröße, wobei oberhalb der Spaltennummerierung z. B. C1000 keine alphanumerischen Einträge bis nahe an Spalte C0 stehen dürfen.
Totzeit-Modelle durch Annäherung mit PT1-Gliedern z. B. 5. Ordnung oder Allpassglieder 3. Ordnung sind möglich.
siehe auch Artikel Totzeit (Regelungstechnik)#Annäherung an das Verhalten eines Totzeitgliedes durch PTn-Glieder als Ersatztotzeit
Numerische Lösung einer zeitabhängigen Funktion, die nicht mit einer DGL beschrieben werden kann[Bearbeiten | Quelltext bearbeiten]
Zahlreiche Anwendungsmodelle sind bekannt, deren Ausgangsgrößen sich auf die unabhängige Variable „Zeit“ beziehen, deren Zeitfolgen durch die Aufgabenstellung festgelegt ist. Die Dimension der Zeitachse hat entweder die Auflösung [s], [Std], [Jahre]. Die bedeutet, dass z. B. die Kapitalanlage von einem Anfangswert aus sich auf die Anzahl von Jahren bezieht. Diese Anzahl entspricht der Schrittweite h.
Darunter fallen die bekannten Aufgabenstellungen wie „Zinseszins“, „Bevölkerungswachstum“, „Flüssigkeitszufluss -Abfluss in Behältern“ und andere.
Diese numerischen Berechnungen sind exakt genau und lassen sich z. B. bei Kapitalanlagen mit der Gleichung der Zinseszinsberechnung leicht überprüfen.
Die numerische Standard-Lösung solcher Aufgaben lässt sich nach Euler-Vorwärts wie folgt berechnen. Bei der exponentiellen Folge wächst oder fällt jedes Folgeglied um einen relativen Anteil. (Beispiel: Zinseszins)
Für einen derartigen Typ Differenzengleichung lässt sich der Wert einer beliebigen Folge direkt algebraisch aus dem Anfangswert berechnen.
Die zugehörige Gleichung als Folge mit dem Verlauf einer Exponentialfunktion mit im Exponenten lautet:

Dabei ist eine Konstante und die Schrittweite.
Statische Übertragungssysteme[Bearbeiten | Quelltext bearbeiten]
Die Anwendungen numerischer Berechnungen mit z. B.: [WENN-, DANN-, SONST]-Anweisungen haben kein Zeitverhalten und können deshalb nicht mit DGL-en berechnet werden.
Bei Verbindung der Anweisungen mit dynamischen Systemen muss die numerische Zuordnung der Folgen beider Systeme gegeben sein.
Das mathematische Modell eines statischen 3-Punktreglers mit Hysterese-Bereich und Totzone wurde numerisch mit 3 verschachtelten „WENN-, DANN-, SONST-Anweisungen“ erstellt. Der Hysteresebereich machte die Funktion einer positiven Rückführung erforderlich. Dieser Regler kann ohne Probleme in Verbindung mit einem numerisch berechneten Modell der Regelstrecke zu einem Regelkreis eingebunden werden. Dynamischen Systeme in der Regelstrecke bedeuten für das Verhalten des Regelkreises eine Näherungslösung.
Der Regler reagiert laut dem beigefügten Diagramm mit der Eingangsgröße = 0,1 bis −0,1 bei der gewählten Schrittweite z. B. in 400 Folgen.
Diese Anwendung mit logischen Anweisungen innerhalb von diskreten Folgen eines Gesamtsystems sind in der Berechnung exakt genau.
In Verbindung mit dynamischen Übertragungssystemen sind die numerischen Gesamtsystem-Berechnungen Annäherungen an die analytische Funktion des Gesamtsystems.
Berechnungsbeispiel einer Steuerstrecke mit einem Totzeitsystem Tt und 4 PT1-Gliedern in Reihe[Bearbeiten | Quelltext bearbeiten]
Die 4 PT1-Glieder befinden sich mit dem Totzeitglied in Reihe, wobei jede Ausgangsgröße die Eingangsgröße des nachfolgenden Systems ist.
Gegeben:
- Schrittweite der Folgeglieder: h = 0,01 [s] gewählt.
- Eingangssignal: Normierter Ansprung bei [s] und Rücksprung bei [s]
- Zugehörige Logik: Start in Spalte C1000:
- Totzeitglied: = 2 [s]; Start in Spalte D1000. Anweisung bezieht sich auf Daten der Spalte C1000.
- INDEX-Anweisung: :
- Zeitglieder: .
- Differenzengleichung PT1-Glied mit Rückwärts-Differenzenquotient:
Beispiel numerische Lösung des -Gliedes mit Zahlenwerten in Spalte E: .
Die nachfolgende Tabelle mit den Folgedaten stellt das diskrete Zeitverhalten nur bis [s] dar.

| Spalte | A Folge k |
B Zeit- folge |
C Eingang Sprung |
D Totzeit Log.0; Log.1 |
E -Glied Folge |
F -Glied Folge |
G -Glied Folge |
H -Glied Folge |
|---|---|---|---|---|---|---|---|---|
| 1000 | 0 | 0 | 1 | 0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 1001 | 1 | 0,01 | 1 | 0 | 0,0 | 0,0 | 0,0 | 0,0 |
| 1200 | 200 | 2,0 | 1 | 1 | 0,0099 | 0,0001 | 0,0 | 0,0 |
| 1201 | 201 | 2,01 | 1 | 1 | 0,0197 | 0,0003 | 0,0 | 0,0 |
| 1202 | 202 | 2,02 | 1 | 1 | 0,0204 | 0,0006 | 0,0 | 0,0 |
| 1203 | 203 | 2,03 | 1 | 1 | 0,0390 | 0,0010 | 0,0 | 0,0 |
| 1204 | 204 | 2,04 | 1 | 1 | 0,0485 | 0,0014 | 0,0 | 0,0 |
| 1205 | 205 | 2,05 | 1 | 1 | 0,0580 | 0,0020 | 0,0001 | 0,0 |
| 1206 | 206 | 2,06 | 1 | 1 | 0,0673 | 0,0026 | 0,0001 | 0,0 |
| 1800 | 800 | 8,0 | 1 | 1 | 0,9975 | 0,9824 | 0,9376 | 0,8484 |
| 1801 | 801 | 8,01 | 1 | 1 | 0,9975 | 0,9826 | 0,9380 | 0,8492 |
siehe auch Artikel Differenzengleichung (Differenzenverfahren).
siehe auch Artikel Numerische Mathematik.
siehe auch Artikel Gewöhnliche Differenzialgleichung.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Andreas Meister, Thomas Sonar: Numerik: Eine lebendige und gut verständliche Einführung mit vielen Beispielen. 1. Auflage. Springer Spektrum, 2018, ISBN 978-3-662-58357-9.
- Bilen Emek Abali, Celal Cakiroglu: Numerische Methoden für Ingenieure, mit Anwendungsbeispielen in Python. Springer Vieweg, 2020, ISBN 978-3-662-61324-5.
- Jürgen Koch, Martin Stämpfle: Mathematik für das Ingenieurstudium. 4. Auflage. Carl Hanser Verlag, München 2018, ISBN 978-3-446-45166-7.
- H.R. Schwarz, N. Klöckner: Numerische Mathematik, Studium, 8. aktualisierte Auflage 2011, Vieweg + Teubner, ISBN 978-3-8348-1551-4.
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. Verlag Europa-Lehrmittel. 12., ergänzte Auflage 2019. ISBN 978-3-8085-5870-6.
- Donald E. Knuth: The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed., Addison-Wesley 1998, ISBN 0-201-89684-2.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ H. Schwarz; Einführung in die moderne Systemtheorie, Vieweg, Berlin, 1969, "Einleitung", ISBN 978-3-322-96127-3
- ↑ Bilen Emek Abali, Celal Cakiroglu: Numerische Methoden für Ingenieure, mit Anwendungsbeispielen in Python. Springer Vieweg, 2020, Hauptkapitel: "Verfahren zur Lösung gewöhnlicher Differenzialgleichungen"
- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink; Verlag: Europa-Lehrmittel, 42781 Haan Gruiten; 12., ergänzte Auflage 2021, Hauptkapitel: "Elemente des Wirkungs- und Signalflussplans"
- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink; Verlag Europa-Lehrmittel, 42781 Haan Gruiten; 12., ergänzte Auflage 2021, Hauptkapitel: "Entwicklung mathematischer Modelle für die Regelungstechnik"
- ↑ Jürgen Dankert; Fachbuchreihe: Numerische Methoden der Mechanik, Einzelfachbuch: „Das Differenzenverfahren“, Springer Vieweg, Berlin, Auszug-Übersicht „Der Grundgedanke des Verfahrens besteht darin, die Differenzialquotienten in Differenzialgleichungen und Randbedingungen durch Differenzenquotienten zu ersetzen.“
- ↑ Lutz / Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink; Hauptkapitel: Übertragungsfunktionen von Regelkreiselementen.


![{\displaystyle k=[0,1,2,3,\dotsc ,k_{\text{max}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7dfbb7225598aae4c29cf213d8960aa4fdc252e)

























![{\displaystyle y_{k+1}=y_{k}\pm y_{k}\cdot C\cdot h.\qquad y_{k=0}={\text{Anfangswert}}\ y_{0},\quad C={\text{Konstante}}\ \neq \ 0,\quad h={\text{Schrittweite}}\ z.B.\ {\text{Laufzeit [Jahre]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3994bbb28cac16a3283eb69902df935247d58de)











![{\displaystyle y_{k+1}=y_{k}+[K_{PT1}\cdot u_{k}-y_{k}]\cdot {\frac {h}{T_{1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02f90659433a570b2a33c772a245a73fec705318)

![{\displaystyle y_{k}=y_{k-1}+[K_{PT1}\cdot u_{k}-y_{k-1}]\cdot {\frac {h}{T_{1}+h}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7b92b29ae938aa9181e4f56b8b500432eb8989)









![{\displaystyle h=0{,}0005\ [s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/550d114a42ab435ccaa4e4533357d678d2364792)







![{\displaystyle PT1_{1},PT1_{2},PT1_{3},PT1_{4}.\qquad {\text{Zeitkonstanten}}\ je\ T1=1[s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71da696930a98a721b9aa3a0f64a52637e980ccb)
![{\displaystyle y_{k}=y_{k-1}+[K_{PT1}\cdot u_{k}-y_{k-1}]\cdot {\frac {h}{T_{1}+h}}.\qquad \qquad y_{k=0}={\text{Anfangswert}}=0;\ y_{k-1}\ {\text{für k = 0}}\ =0;\ h=0,01[s]={\text{Schrittweite}};\ K_{PT1}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f7624ca50480cd4aa181733ebdd847fe235881f)

![{\displaystyle \ t_{k}=2\ [s];\ k=200;\ u_{k}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0e1c2fe3ab06679b2f9bec5a48976e0f80e7b95)
![{\displaystyle y_{k=200}=y_{k=199}+[u_{k=200}-y_{k=199}]\cdot {\frac {0{,}01}{1+0{,}01}}=0{,}0+[1-0]\cdot 0{,}0099=0{,}0099}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab2d21a83259ca83de2840418c973a4539ce7d1b)
![{\displaystyle y_{k=201}=y_{k=200}+[u_{k=201}-y_{k=200}]\cdot {\frac {0{,}01}{1+0{,}01}}=0,0099+[1-0{,}0099]\cdot 0{,}0099=0{,}0197}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae78014e2854bbb9454c18441bdfc7e1797b3334)


![{\displaystyle T=1\ [s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf0dd6e2f8d85fca6bfd673b4276012f8e463cfd)
![{\displaystyle t_{k}[s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22231afe2859b7d3938e861e945cecefd2d978d7)







