Umfüllrätsel
Umfüllrätsel sind eine bekannte Gattung von Denksportaufgaben. In der einfachsten Version kommen darin drei Gefäße mit bekanntem Volumen vor, von denen zu Beginn eines vollständig mit Wasser gefüllt ist, während die beiden anderen leer sind. Ziel ist es bestimmte Wassermengen abzumessen. Da die Gefäße aber keine Skala besitzen, muss der Abmessvorgang durch mehrfaches Umfüllen geschehen.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Ältestes und zugleich bekanntestes Beispiel für ein Umfüllrätsel ist die folgende Aufgabe: Ein Gefäß, das 8 Liter fasst, ist bis zum Rand mit Wasser gefüllt. Daneben stehen noch zwei weitere Gefäße, die 3 bzw. 5 Liter fassen, beide leer. Wie kann man durch wiederholtes Umfüllen genau 4 Liter abmessen, also sowohl im 5- wie im 8-Liter-Gefäß jeweils 4 Liter Wasser haben?
Zur Lösung kann man die einzelnen Zustände als Tripel notieren, indem man angibt, wie viele Liter sich in den einzelnen Gefäßen (in der Reihenfolge 3, 5, 8) befinden. Der Ausgangszustand ist dann (0, 0, 8), der gewünschte Endzustand (0, 4, 4).
- Zunächst füllt man das 5-Liter-Gefäß aus dem 8-Liter-Gefäß bis zum Rand, zurück bleiben 3 Liter: (0, 5, 3)
- Aus dem 5-Liter-Gefäß füllt man das 3-Liter-Gefäß bis zum Rand: (3, 2, 3)
- Das 3-Liter-Gefäß entleert man in das 8-Liter-Gefäß: (0, 2, 6)
- Den Inhalt des 5-Liter-Gefäßes schüttet man in das 3-Liter-Gefäß: (2, 0, 6)
- Man füllt das 5-Liter-Gefäß erneut aus dem 8-Liter-Gefäß: (2, 5, 1)
- Man füllt das 3-Liter-Gefäß aus dem 5-Liter-Gefäß auf: (3, 4, 1)
- Man schüttet den Inhalt des 3-Liter-Gefäßes in das 8-Liter-Gefäß zurück: (0, 4, 4)
Geschichte[Bearbeiten | Quelltext bearbeiten]
Die erste schriftliche Überlieferung für ein Umfüllproblem findet sich in der Chronik Annales Stadenses, die Albert von Stade im 13. Jahrhundert zusammenstellte.[1] Beim Eintrag für das Jahr 1152 sind einige Rätsel eingefügt, darunter auch das obige Umfüllrätsel. Im 16. Jahrhundert beschäftigte sich Niccolò Tartaglia mit diesen Problemen, sodass sie häufig ihm zugeschrieben werden. 1917 schrieb der Rätselexperte Henry Dudeney, dass solche Aufgaben bisher nur mit Versuch und Irrtum gelöst wurden, er aber glaube, dass es zumindest für Spezialfälle Formeln gäbe.[2] 1939 gab M. C. K. Tweedie eine systematische Lösung.[3] Im 20. Jahrhundert verwendete Abraham S. Luchins Aufgaben dieses Typs in psychologischen Experimenten.
Mathematische Analyse[Bearbeiten | Quelltext bearbeiten]
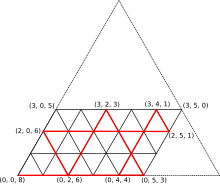
Zur Analyse von Umfüllrätseln setzte Tweedie trilineare Koordinaten ein. Das obige Beispiel kann an einem gleichseitigen Dreieck mit der Höhe 8 gelöst werden, die Füllmengen bezeichnen Punkte in diesem Dreieck, wenn man sie als Trilinearkoordinaten liest. Da die beiden ersten Gefäße nur 3 bzw. 5 Liter enthalten können, entsprechen nicht allen Punkten des Dreiecks gültige Füllzustände, die zulässigen Punkte bilden ein Parallelogramm, das im Dreieck enthalten ist. Beim Umfüllen bleibt immer ein Gefäß unberührt, sodass man sich dabei auf Parallelen zu den Seiten des Dreiecks bewegt. Außerdem muss beim Umfüllen immer ein Gefäß vollständig geleert oder gefüllt werden, sodass der Pfad im Parallelogramm immer bis zu dessen Rand geht. Tatsächlich ist der Pfad bereits durch den ersten Schritt festgelegt, alle weiteren Schritte ergeben sich automatisch.
Bei anderen Gefäßgrößen kann sich statt des Parallelogramms auch ein unregelmäßiges Fünf- oder Sechseck[4] ergeben, die Lösungsidee bleibt jedoch die gleiche.
Der Pfad hat die Besonderheit, dass der Eintritts- und Austrittswinkel in den Randpunkten immer übereinstimmt. Man kann ihn sich also als Weg einer idealen Billardkugel auf einem parallelogrammförmigen Tisch vorstellen.
Mit mehr als drei Gefäßen ist eine analoge Lösung möglich, die Figuren liegen dabei in entsprechend höherdimensionalen Räumen.
Eine algebraische Lösung stammt von Paolo Boldi, Massimo Santini und Sebastiano Vigna.[5] Diese Analyse gibt auch obere und untere Schranken für die Zahl der notwendigen Umfüllungen an.
Trivia[Bearbeiten | Quelltext bearbeiten]
In Stirb langsam: Jetzt erst recht (Originaltitel: Die Hard with a Vengeance) kommt ein Umfüllrätsel vor. Deswegen sind Umfüllrätsel im Englischen auch als Die Hard with a Vengeance puzzle bekannt.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Heinrich Hemme: Kopfnuss. 101 mathematische Rätsel aus vier Jahrtausenden und fünf Kontinenten. Verlag C.H. Beck, 2012. ISBN 978-3-406-63704-9. S. 30.
- ↑ Henry Ernest Dudeney: Amusements in Mathematics. 1917. S. 109. (Amusements in Mathematics im Project Gutenberg )
- ↑ M. C. K. Tweedie: A Graphical Method of Solving Tartaglian Measuring Puzzles. In: The Mathematical Gazette. Vol. 23, Nr. 255, Juli 1939. S. 278–282. (JSTOR:3606420)
- ↑ Alexander Bogomolny: Barycentric coordinates, three jugs application. Abgerufen am 29. April 2018.
- ↑ Paolo Boldi, Massimo Santini und Sebastiano Vigna: Measuring with Jugs. In: Theoretical Computer Science. 282(2), 2002. S. 259–270.(online, PDF)