Benutzer:Hightower74/Exponentialfunktion
In der Mathematik bezeichnet man als Exponentialfunktion eine Funktion der Form mit einer reellen Zahl als Basis (Grundzahl). In der gebräuchlichsten Form sind dabei für den Exponenten die reellen Zahlen zugelassen. Im Gegensatz zu den Potenzfunktionen, bei denen die Basis die unabhängige Größe (Variable) und der Exponent fest vorgegeben ist, ist bei Exponentialfunktionen der Exponent (auch Hochzahl) des Potenzausdrucks die Variable und die Basis fest vorgegeben. Darauf bezieht sich auch die Namensgebung. Exponentialfunktionen haben in den Naturwissenschaften, z. B. bei der mathematischen Beschreibung von Wachstumsvorgängen, eine herausragende Bedeutung (siehe exponentielles Wachstum).
Als natürliche Exponentialfunktion oder e-Funktion bezeichnet man die Exponentialfunktion mit der eulerschen Zahl als Basis; gebräuchlich hierfür ist auch die Schreibweise . Diese Funktion hat gegenüber den anderen Exponentialfunktionen besondere Eigenschaften. Unter Verwendung des natürlichen Logarithmus lässt sich mit der Gleichung jede Exponentialfunktion auf eine solche zur Basis zurückführen. Deshalb befasst sich dieser Artikel im Wesentlichen mit der Exponentialfunktion zur Basis .

Definition[Bearbeiten | Quelltext bearbeiten]
Die Exponentialfunktion zu der Basis kann auf den reellen Zahlen auf verschiedene äquivalente Weisen definiert werden.
Elementare axiomatische Definition[Bearbeiten | Quelltext bearbeiten]
Eine einfache Art die Exponentialfunktion ohne Rückgriff auf analytische Konzepte wie etwa Folgen, Reihen, Grenzwerte o.ä. zu definieren ist die Charakterisierung über ihre Grundeigenschaften:
1. Funktionalgleichung
2. Abschätzung nach unten
Es lässt sich zeigen, dass die durch diese Eigenschaften beschriebene Funktion existiert und eindeutig bestimmt ist.
Definition als Grenzwert einer Folge[Bearbeiten | Quelltext bearbeiten]
Sehr wichtig ist die Definition als Grenzwert einer Folge mit :
Auf diese Weise lässt sich auch die komplexe Exponentialfunktion definieren.
Definition als Potenzreihe[Bearbeiten | Quelltext bearbeiten]
Von zentraler Bedeutung ist die Definition als Potenzreihe, die sogenannte Exponentialreihe
- ,
wobei die Fakultät von bezeichnet.
Diese Variante wird normalerweise verwendet, um die komplexe Exponentialfunktion zu definieren (siehe weiter unten).
Definition als Lösung eines Anfangswertproblems[Bearbeiten | Quelltext bearbeiten]
Schließlich kann man die Exponentialfunktion auch als Lösung eines Anfangswertproblems charakterisieren:
1. Differentialgleichung
2. Anfangswert
Auch hier lässt sich zeigen, dass durch diese beiden Bedingungen eindeutig festgelegt wird und existiert.
Grundlegende Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Die reelle Exponentialfunktion ist positiv, stetig, streng monoton wachsend und surjektiv. Dabei bezeichnet die Menge der positiven reellen Zahlen. Sie ist folglich bijektiv. eshalb existiert ihre Umkehrfunktion, der natürliche Logarithmus . Daraus erklärt sich auch die Bezeichnung Antilogarithmus für die Exponentialfunktion.
1. Positivität
2. Strenge Monotonie
3. Verhalten im Unendlichen
4. Verhalten im negativ-Unendlichen
5. Abschätzung nach oben
Aus der Abschätzung nach unten (siehe axiomatische Charakterisierung) erhält man durch Einsetzen von auch leicht eine obere Schranke für alle :
Konvergenz der Reihe, Stetigkeit[Bearbeiten | Quelltext bearbeiten]

Die punktweise Konvergenz der für die Definition der Exponentialfunktion verwendeten Reihe
lässt sich für alle reellen und komplexen einfach mit dem Quotientenkriterium zeigen; daraus folgt sogar absolute Konvergenz. Der Konvergenzradius der Potenzreihe ist also unendlich. Da Potenzreihen an jedem inneren Punkt ihres Konvergenzbereiches analytisch sind,[1] ist die Exponentialfunktion also in jedem reellen und komplexen Punkt trivialerweise auch stetig.[2]
Rechenregeln[Bearbeiten | Quelltext bearbeiten]
Da die Exponentialfunktion die Funktionalgleichung erfüllt, kann man mit ihrer Hilfe das Potenzieren auf reelle und komplexe Exponenten verallgemeinern, indem man definiert:
für alle und alle reellen oder komplexen .
Generell gilt diese Umformung von auch für beliebige andere Werte als neue Basis:
Solche Funktionen heißen exponentielle Funktionen und „verwandeln“ Multiplikation in Addition. Genauer zeigen das die folgenden Potenzgesetze:
- und
Diese Gesetze gelten für alle positiven reellen und und alle reellen und . Ausdrücke mit Brüchen und Wurzeln können oft mit Hilfe der Exponentialfunktion vereinfacht werden:
Siehe auch Rechenregeln für Logarithmus.
Ableitung[Bearbeiten | Quelltext bearbeiten]
Die große Bedeutung der e-Funktion, eben die Exponentialfunktion mit Basis , beruht auf der Tatsache, dass ihre Ableitung wieder die Funktion selbst ergibt:
Wenn man zusätzlich
fordert, ist die e-Funktion sogar die einzige Funktion , die dies leistet. Somit kann man die e-Funktion auch als Lösung dieser Differentialgleichung f'(x) = f(x) mit dieser Anfangsbedingung f(0) = 1 definieren.
Allgemeiner folgt für reelles aus
und der Kettenregel die Ableitung beliebiger Exponentialfunktionen:
In dieser Formel kann der natürliche Logarithmus nicht durch einen Logarithmus zu einer anderen Basis ersetzt werden; die Zahl e kommt also in der Differentialrechnung auf „natürliche“ Weise ins Spiel.
Stammfunktion[Bearbeiten | Quelltext bearbeiten]
Aus den Ergebnissen über die Ableitung ergibt sich die Stammfunktion der e-Funktion:
- .
Für beliebige Exponentialfunktionen mit und gilt:
- .
Exponentialfunktion auf den komplexen Zahlen[Bearbeiten | Quelltext bearbeiten]



Mit Hilfe der Reihendarstellung
lässt sich die Exponentialfunktion für komplexe Zahlen definieren. Die Reihe konvergiert für alle absolut.
Die Exponentialfunktion behält für alle komplexen Zahlen , folgende wichtige Eigenschaften:
Die Exponentialfunktion ist somit ein surjektiver, aber nicht injektiver Gruppenhomomorphismus von der abelschen Gruppe auf die abelsche Gruppe , also von der additiven auf die multiplikative Gruppe des Körpers .
In hat die Exponentialfunktion eine wesentliche Singularität, ansonsten ist sie holomorph, d. h., sie ist eine ganze Funktion. Die komplexe Exponentialfunktion ist periodisch mit der komplexen Periode , es gilt also
Beschränkt man ihren Definitionsbereich auf einen Streifen
mit , dann besitzt sie eine wohldefinierte Umkehrfunktion, den komplexen Logarithmus.
Die Exponentialfunktion kann zur Definition der trigonometrischen Funktionen für komplexe Zahlen verwendet werden:
Dies ist äquivalent zur eulerschen Formel
- .
Daraus abgeleitet ergibt sich speziell die Gleichung
der in Physik und Technik wichtigen komplexen Exponentialschwingung mit der Kreisfrequenz und der Frequenz .
Ebenso kann die Exponentialfunktion zur Definition der hyperbolischen Funktionen verwendet werden:
Man kann auch im Komplexen eine allgemeine Potenz definieren:
- mit .
Die Werte der Potenzfunktion sind dabei abhängig von der Wahl des Einblättrigkeitsbereichs des Logarithmus, siehe auch Riemannsche Fläche. Dessen Mehrdeutigkeit wird ja durch die Periodizität seiner Umkehrfunktion, eben der Exponentialfunktion, verursacht. Deren grundlegende Gleichung
entspringt der Periodizität der Exponentialfunktion mit reellem Argument . Deren Periodenlänge ist genau der Kreisumfang des Einheitskreises, den die Sinus- und Kosinusfunktionen wegen der Eulerschen Formel beschreiben. Die Exponential-, die Sinus- und die Kosinusfunktion sind nämlich nur Teile derselben (auf komplexe Zahlen verallgemeinerten) Exponentialfunktion, was im Reellen nicht offensichtlich ist.
Exponentialfunktion auf beliebigen Banachalgebren[Bearbeiten | Quelltext bearbeiten]
Die Exponentialfunktion lässt sich auf Banachalgebren, zum Beispiel Matrix-Algebren mit einer Operatornorm, verallgemeinern. Sie ist dort ebenfalls über die Reihe
definiert, die für alle beschränkten Argumente aus der jeweils betrachteten Banachalgebra absolut konvergiert.
Die wesentliche Eigenschaft der reellen (und komplexen) Exponentialfunktion
ist in dieser Allgemeinheit allerdings nur noch gültig für Werte und , die kommutieren, also für Werte mit (dies ist in den reellen oder komplexen Zahlen natürlich immer erfüllt, da die Multiplikation dort kommutativ ist). Einige Rechenregeln dieser Art für die Exponentiale von linearen Operatoren auf einem Banachraum liefern die Baker-Campbell-Hausdorff-Formeln.
Eine wichtige Anwendung dieser verallgemeinerten Exponentialfunktion findet sich beim Lösen von linearen Differentialgleichungssystemen der Form mit konstanten Koeffizienten. In diesem Fall ist die Banachalgebra die Menge der -Matrizen mit komplexen Einträgen. Mittels der jordanschen Normalform lässt sich eine Basis bzw. Ähnlichkeitstransformation finden, in welcher die Exponentialmatrix eine endliche Berechnungsvorschrift hat. Genauer gesagt, man findet eine reguläre Matrix , so dass , wobei eine Diagonalmatrix und eine nilpotente Matrix sind, welche miteinander kommutieren. Es gilt damit
Das Exponential einer Diagonalmatrix ist die Diagonalmatrix der Exponentiale, das Exponential der nilpotenten Matrix ist ein matrixwertiges Polynom mit einem Grad, der kleiner als die Dimension der Matrix ist.
Numerische Berechnungsmöglichkeiten[Bearbeiten | Quelltext bearbeiten]
Als fundamentale Funktion der Analysis wurde viel über Möglichkeiten zur effizienten Berechnung der Exponentialfunktion bis zu einer gewünschten Genauigkeit nachgedacht. Dabei wird stets die Berechnung auf die Auswertung der Exponentialfunktion in einer kleinen Umgebung der Null reduziert und mit dem Anfang der Potenzreihe gearbeitet. In der Analyse ist die durch die Reduktion notwendige Arbeitsgenauigkeit gegen die Anzahl der notwendigen Multiplikationen von Hochpräzisionsdaten abzuwägen.
Der Rest der -ten Partialsumme hat eine einfache Abschätzung gegen die geometrische Reihe, welche auf
- bei für alle mit führt.
Die einfachste Reduktion benutzt die Identität , d. h. zu gegebenem wird bestimmt, wobei nach den Genauigkeitsbetrachtungen gewählt wird. Damit wird nun, in einer gewissen Arbeitsgenauigkeit, berechnet und -fach quadriert: . wird nun auf die gewünschte Genauigkeit reduziert und als zurückgegeben.
Effizientere Verfahren setzen voraus, dass , besser zusätzlich und (Arnold Schönhage) in beliebiger (nach Spezifikation auftretender) Arbeitsgenauigkeit verfügbar sind. Dann können die Identitäten
- oder
benutzt werden, um auf ein aus dem Intervall oder einem wesentlich kleineren Intervall zu transformieren und damit das aufwändigere Quadrieren zu reduzieren oder ganz zu vermeiden.
Bei Implementierung in Hardware werden für deren Belange geeignete Verfahren genutzt, zum Beispiel:
Hintergründe und Beweise[Bearbeiten | Quelltext bearbeiten]
Motivation[Bearbeiten | Quelltext bearbeiten]
Auf die natürliche Exponentialfunktion stößt man, wenn man von den Grundeigenschaften aus der axiomatischen Definition ausgeht. Mit der unteren Schranke aus der Definition und der daraus ableitbaren oberen Schranke erhält man folgende Ungleichungskette für angewendet auf das Argument :
Potenzieren mit führt dann auf Grund der Funktionalgleichung und der Monotonie der Potenzfunktion für positive Argumente auf:
Dies kann man auch als Intervallschachtelung
für die gesuchte Funktion auffassen, wobei die Folge der unteren und die folge der oberen Intervallgrenzen bezeichnet.
Die untere Schranke für entpspricht gerade der Definition als Folge.
Es sind num im folgenden die Eindeutigkeit (Konvergenz der Folgen und gegen den gleichen Grenzwert) sowie die Existenz von (Gültigkeit der Funktionalgleichung und der Abschätzung nach Unten für den Limes) zu zeigen.
Beweis der Eindeutigkeit[Bearbeiten | Quelltext bearbeiten]
Dass die in der Motivation definierten Folgen und tatsächlich eine Intervallschachtelung für bilden, muss bewiesen werden, d.h. wir müssen nachweisen, dass die drei charakteristischen Eigenschaften einer Intervallschachtelung erfüllt sind:
1. Intervalleigenschaft:
2. Monotonie der Folgen der unteren Intervallgrenzen und oberen Intervallgrenzen
3. Die Folge der Intervalllängen ist eine Nullfolge, d.h.
Der Nachweis dieser drei Eigenschaften zeigt zunächst nur die Eindeutigkeit es Objektes , d.h. falls existiert, dann ist es eindeutig bestimmt. Die Existenz des Objektes (d.h. die Gültigkeit der Funktionalgleichung für die Grenzfunktion) muss dann noch zusätzlich bewiesen werden.
Intervalleigenschaft[Bearbeiten | Quelltext bearbeiten]
Die rechte Ungleichung ist auf jeden Fall richtig, falls . Dies überträgt sich entsprechend auf die anderen Ungleichungen der Äquivalenzkette, insbesondere auf die zu beweisende Aussage, dass die obere Intervallgrenze immer grösser (oder gleich) als ihr entsprechendes Gegenstück ist.
Monotones Wachstum der Folge der unteren Intervallgrenzen[Bearbeiten | Quelltext bearbeiten]
Sei fest gewählt. Dann gilt für
beziehungsweise
Für gelten diese Ungleichungen für
In der Abschätzung wird die Bernoullische Ungleichung verwendet, die wegen anwendbar ist, sofern . Damit ist nachgewiesen, dass die Folge der unteren Intervallgrenzen monoton wachsend ist.
Monotones Abnehmen der Folge der oberen Intervallgrenzen[Bearbeiten | Quelltext bearbeiten]
Das im vorherigen Abschnitt nachgewiesene monotone Wachstum für gilt unabhängig vom Vorzeichen von , d.h. auch die Folge
ist monoton wachsend. Da nun die Folge der oberen Intervallgrenzen gerade der Kehrwert von ist, folgt direkt, dass eine monoton fallende folge ist.
Beschränktheit und Konvergenz der Folgen der Intervallgrenzen[Bearbeiten | Quelltext bearbeiten]
Wir bezeichnen mit . Auf Grund der Intervalleigenschaft (s.o.) und der Monotonie von und gelten folgende Abschätzungen:
Aus der Beschränktheit und den bereits zuvor nachgewiesenen Monotonieeigenschaften folgt nach dem Monotoniekriterium, dass beide Folgen auch konvergent sind.
Folge der Intervall-Längen konvergiert gegen Null[Bearbeiten | Quelltext bearbeiten]
Es bleibt noch zu zeigen, dass die Folgen und gegen den gleichen Grenzwert konvergieren, oder in anderen Worten dass die Folge der Intervall-Längen
gegen Null konvergiert.
Da gegen einen Wert konvergiert, reicht es aus, die Folge
zu untersuchen, die wir bereits weiter oben im Zusammenhang mit der Intervalleigenschaft betrachtet haben und für die wir festgestellt haben, dass für .
Anwenden der Bernoullischen Ungleichung für liefert dann folgende Einschliessung für :
Nach dem Einschnürungssatz folgt, dass .
Beweis der Existenz[Bearbeiten | Quelltext bearbeiten]
Wie bereits weiter oben erwähnt muss man für die Existenz noch zeigen, dass der Grenzwert der Folge tatsächlich die geforderten Axiome, d.h. die Funktionalgleichung und die Abschätzung nach unten, erfüllt.
Funktionalgleichung[Bearbeiten | Quelltext bearbeiten]
Da , und konvergieren, konvergiert auch der Quotient
Hierbei können wir uns die allgemeine Tatsache zunutze machen, dass für eine beliebige Nullfolge folgender Grenzwert gilt:
Abschätzung nach unten[Bearbeiten | Quelltext bearbeiten]
Für ist die Voraussetzung für die Anwendbarkeit der Bernoullischen Ungleichung, d.h. auf jeden Fall erfüllt und man kann folgendermassen abschätzen:
Diese Abschätzung gilt insbesondere auch nach Übergang zum Grenzwert durch .
Äquivalenz zwischen Defintion als Folge und elementarer Defintion[Bearbeiten | Quelltext bearbeiten]
Die obigen Rechnungen und Ausführungen zeigen gerade die Äquivalenz der beiden Definitionen.
Äquivalenz zwischen Defintion als Potenzreihe und elementrarer Defintion[Bearbeiten | Quelltext bearbeiten]
Es reicht aus nachzuweisen, dass die Potenzreihendarstellung die Axiome der elementaren Definition erfüllt - unter der Voraussetzung dass die Reihendarstellung wohl-definiert ist. Dazu muss man zeigen, dass die Potenzreihe konvergiert:
Konvergenz der Potenzreihe[Bearbeiten | Quelltext bearbeiten]

Die absolute Konvergenz der für die Definition der Exponentialfunktion verwendeten Reihe
lässt sich für alle reellen und komplexen einfach mit dem Quotientenkriterium zeigen; der Konvergenzradius der Potenzreihe ist also unendlich. Da Potenzreihen an jedem inneren Punkt ihres Konvergenzbereiches analytisch sind,[3] ist die Exponentialfunktion also in jedem reellen und komplexen Punkt trivialerweise auch stetig.[2]
Funktionalgleichung[Bearbeiten | Quelltext bearbeiten]
Durch Anwenden des Binomischen Lehrsatzes und der Defintion des Binomialkoeffizienten auf die einzelnen Glieder der Reihe erhält man:
Andererseits sind die Voraussetzungen für die Anwendung der Cauchy-Produktformel erfüllt, da da die Reihen und absolut konvergieren, d.h. es gilt:
Beide Terme sind also gleich und damit folgt die Gültigkeit der Funktionalgleichung.
Abschätzung nach unten[Bearbeiten | Quelltext bearbeiten]
Für folgt direkt aus der Definition der Reihe die Abschätzung . Insbesondere lässt sich aus der Funktionalgleichung ableiten, dass die Positivität von auch für negative gilt. Es reicht also aus, die Gültigkeit der Abschätzung auf auszudehnen. Für lässt sich die Reihe folgendermassen umschreiben und entsprechend abschätzen:
Damit folgt für alle die Gültigkeit der Abschätzung.
Äquivalenz zwischen Definition als Potenzreihe und Definition als Lösung eines Afangswertproblems[Bearbeiten | Quelltext bearbeiten]
Potenzreihe löst das Anfangswertproblem[Bearbeiten | Quelltext bearbeiten]
Wie bereits oben gezeigt, ist die Funkion (definiert als Potenzreihe) analytisch. Daher können wir die Ableitung von durch gliedweise Differentiation der Potenzreihe ermitteln:
Da aus der Definition der Potenzreihe sofort folgt, ist nachgewiesen, dass das Anfangswertproblem löst.
Anfangswertproblem führt auf Potenzreihe[Bearbeiten | Quelltext bearbeiten]
Durch vollständige Induktion folgt unmittelbar auch sowie . Damit lässt sich in eine Taylorreihe entwickeln, die gerade der Definition als Potenzreihe entspricht.
Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Abschätzung nach unten[Bearbeiten | Quelltext bearbeiten]
Für reelle lässt sich die Exponentialfunktion mit
nach unten abschätzen. Der Beweis ergibt sich aus der Definition
und der Tatsache, dass für hinreichend große . Da die Folge monoton wachsend ist, ist der Grenzwert daher echt größer Null.
Diese Abschätzung lässt sich zur wichtigen Ungleichung
verschärfen. Für folgt sie aus , für ergibt sich der Beweis beispielsweise, indem man die bernoullische Ungleichung auf die Definition
anwendet. Eine Anwendung dieser Ungleichung ist der Polya-Beweis der Ungleichung vom arithmetischen und geometrischen Mittel. Allerdings erleichtert die Ungleichung vom arithmetischen und geometrischen Mittel die Untersuchung der Folge sehr; um daher einen Zirkelschluss zu vermeiden, benötigt der Polya-Beweis Herleitungen der Exponentialfunktion, die ohne Ungleichung vom arithmetischen und geometrischen Mittel auskommen.
Abschätzung nach oben[Bearbeiten | Quelltext bearbeiten]
Setzt man in der Abschätzung nach unten statt ein und verwendet , so erhält man durch Umstellen der Ungleichung die für alle gültige Abschätzung nach oben .
Ableitung der Exponentialfunktion[Bearbeiten | Quelltext bearbeiten]
Die wichtigste Anwendung dieser beiden Abschätzungen ist die Berechnung der Ableitung der Exponentialfunktion an der Stelle 0:
Gemeinsam mit der Funktionalgleichung folgt daraus die Ableitung der Exponentialfunktion für beliebige reelle Zahlen:
Wachstum der e-Funktion im Vergleich zu Polynomfunktionen[Bearbeiten | Quelltext bearbeiten]
Oft wird die Aussage benötigt, dass die Exponentialfunktion wesentlich stärker wächst als jede Potenzfunktion, d. h.
Für ist dies klar, für kann entweder induktiv die Regel von de L’Hospital benutzt werden, oder auch elegant abgeschätzt werden:
Zunächst gilt
Wegen gilt
Dies konvergiert gegen und somit der obige Grenzwert gegen 0.
Basiswechsel[Bearbeiten | Quelltext bearbeiten]
Wie bereits zuvor erwähnt, gilt
Beweis: Nach Definition des Logarithmus ist äquivalent zu , woraus die Identität folgt. Ersetzen von durch liefert
wobei im zweiten Schritt die Logarithmus-Rechenregel für Potenzen angewendet wurde.
Die Differentialgleichung der Exponentialfunktion[Bearbeiten | Quelltext bearbeiten]
Will man die einfache Differentialgleichung: lösen und setzt noch voraus, so erhält man daraus eine Definition von .
Umkehrfunktion[Bearbeiten | Quelltext bearbeiten]
Setzt man nicht voraus, so benutzt man die Umkehrfunktion von
Denn , und nach den Eigenschaften der Logarithmusfunktion ist
und man kann die Umkehrfunktion bilden und erhält
Da die untere Grenze gleich 1 ist, ist und bei der Umkehrfunktion nach Eigenschaft der Umkehrfunktion: .
Differentialgleichung[Bearbeiten | Quelltext bearbeiten]

Erweitert man die Differentialgleichung auf für und löst sie, so erhält man für die Form
Speziell für ist
Ist dann eine Lösung und , dann ist
und nach Voraussetzung
Für beliebiges führen wir
ein. Es ergibt sich
und nach Voraussetzung wieder
Man besitzt nun ein Instrument zur Beschreibung von Vorgängen in verschiedenen Bereichen der Wissenschaft, in denen man mittels eines Ansatzes vom Typ ein Ergebnis der Form erhält, welches auf der Exponentialfunktion basiert.
Beispiele für Exponentialfunktionen[Bearbeiten | Quelltext bearbeiten]
Physik[Bearbeiten | Quelltext bearbeiten]
Als Beispiele für das häufige Auftreten der Exponentialfunktion in der Physik seien genannt:
- der radioaktive Zerfall von Teilchen
- der Luftdruckverlauf in der Atmosphäre siehe barometrische Höhenformel
- zeitliche Ladungskurven eines elektrischen Kondensators
- zeitliche Energiekurve beim Einschaltvorgang einer Spule durch Selbstinduktion
- Thermodynamik und Statistik: Boltzmann-Faktor, Fermi-Dirac-Statistik, Bose-Einstein-Statistik
- die Abkühlung und Erwärmung eines Körpers
Chemie[Bearbeiten | Quelltext bearbeiten]
Als ein Beispiel in der Chemie sei hier eine einfache chemische Reaktion skizziert. Es wird angenommen, dass wir die Lösung eines Stoffes vorliegen haben, etwa Rohrzucker in Wasser. Der Rohrzucker werde nun durch einen Katalysator zu Invertzucker umgewandelt (hydrolysiert). Bei dieser einfachen chemischen Reaktion wird man das Geschwindigkeitsgesetz (unter Vernachlässigung der Rückreaktion) wie folgt formulieren:
- Die Reaktionsgeschwindigkeit als Funktion der Zeit ist proportional zur noch vorhandenen Menge der sich umwandelnden Substanz.
Bezeichnen wir die Menge des zur Zeit noch nicht umgewandelten Rohrzuckers mit , so ist die Reaktionsgeschwindigkeit , und nach dem oben formulierten Geschwindigkeitsgesetz gilt die Gleichung
mit einer reaktionsspezifischen Geschwindigkeitskonstante . Aus diesem Momentangesetz erhält man nach obiger Differentialgleichung ein Integralgesetz, welches uns die Menge des übriggebliebenen Rohrzuckers als Funktion der Zeit liefert:
wobei die Konstante die zur Zeit vorhandene Menge bezeichnet. Die chemische Reaktion nähert sich also asymptotisch ihrem Endzustand an, der völligen Umwandlung von Rohrzucker in Invertzucker. (Die Vernachlässigung der Rückreaktion ist hier akzeptabel, da das chemische Gleichgewicht der Rohrzucker-Hydrolyse sehr stark auf Seiten des Invertzuckers liegt).
Biologie, Epidemien[Bearbeiten | Quelltext bearbeiten]
Beschreibung des exponentiellen Wachstums in der Anfangszeit einer Population von z. B. Mikroorganismen, Ausbreitung von Infektionen im Rahmen einer Epidemie und Fortpflanzung von Lebewesen, siehe r-Strategie oder SIR-Modell.
Stochastik[Bearbeiten | Quelltext bearbeiten]
- Gleiche Anzahl von Münzen und Empfängern
Wie groß sind die Wahrscheinlichkeiten, zufällig keine, eine oder mehr Münzen zu erhalten, wenn Münzen zufällig auf Empfänger verteilt werden und sehr groß ist?
Die Definitionsformel für die Exponentialfunktion
- ,
die daraus abgeleitete Näherungsformel
und die eulersche Zahl erlauben eine einfache Abschätzung.
Die Wahrscheinlichkeit, bei der ersten Verteilung eine Münze zu erhalten, beträgt und , keine Münze zu erhalten. Die Wahrscheinlichkeit, zweimal keine Münze zu erhalten, beträgt: . Folglich ist die Wahrscheinlichkeit, -mal erfolglos zu sein:
Die Wahrscheinlichkeit, nur einmal Erfolg zu haben, ist das Produkt aus Misserfolgen, Erfolg und der Kombinationsmöglichkeiten , wann sich der Erfolg einstellt (beim ersten Mal, oder zweiten oder dritten …):
Die Wahrscheinlichkeit, mehr als eine Münze zu erhalten, lautet entsprechend:
- Mehr Münzen als Empfänger
Wie viele Münzen müssen es sein, um die Wahrscheinlichkeit , keine zu erhalten, zu verringern, beispielsweise auf 0,1 statt 0,37? Aus obiger Näherungsformel folgt:
Oder anders gefragt: Wie viele Münzen müssen es mehr sein als Empfänger ?
Damit im Mittel nur 10 % der Empfänger leer ausgehen, ist die 2,3-fache Menge an Münzen erforderlich, bei 1 % fast die 5-fache Anzahl.
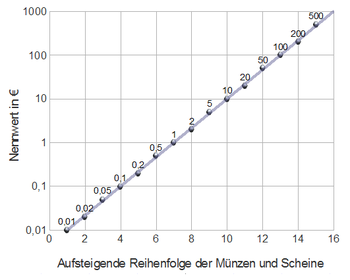
Wirtschaft[Bearbeiten | Quelltext bearbeiten]
- Stetige Verzinsung
- Die Stückelung folgt üblicherweise einer exponentiellen Gesetzmäßigkeit beim Anstieg des Wertes. Am Beispiel des Euro ist zu den Punkten für jede Münze oder Banknote eine Ausgleichsgerade dargestellt. Die geringen Abweichungen von dieser Geraden folgen aus der Forderung nach „runden“ Zahlen, die mit nur einer signifikanten Stelle exakt anzugeben sind (nicht zu verwechseln mit glatten Zahlen).
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Wenn eine Größe ist, deren Potenzen für beliebiges nicht-negatives ganzzahliges existieren, und wenn der Grenzwert existiert, ist es sinnvoll, die abstrakte Größe durch die oben angegebene Exponentialreihe zu definieren. Ähnliches gilt für Operatoren , die, einschließlich ihrer Potenzen, eine lineare Abbildung eines Definitionsbereichs eines abstrakten Raumes (mit Elementen ) in einen Wertebereich der reellen Zahlen ergeben: Hier ist es sogar für alle reellen sinnvoll, in ganz (genauer: im zugehörigen Abschlussbereich) Exponentialoperatoren durch den Ausdruck zu definieren, wobei die Konvergenz dieses Ausdrucks zunächst offenbleibt.
Iteration der Exponentiation führt auf die Verallgemeinerte Exponentialfunktion, die in der Gleitkomma-Arithmetik verwendet wird.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Die e-Funktion für Schüler erklärt
- Interaktives Java-Applet: Vergleich verschiedener Basen a mit a>1
- Ausführliche Erklärung der Exponential- bzw. Logarithmusfunktion
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Christian Blatter, Analysis II. 1. Auflage, Springer Verlag 1974, ISBN 3-540-06914-3, Kap. 18, § 182, Potenzreihen
- ↑ a b Konrad Knopp. Theorie und Anwendung der unendlichen Reihen. 5. Auflage, Springer Verlag 1964, ISBN 3-540-03138-3. S 175, 98 Satz 2 für den reellen und S 418 für den komplexen Fall
- ↑ Christian Blatter, Analysis II. 1. Auflage, Springer Verlag 1974, ISBN 3-540-06914-3, Kap. 18, § 182, Potenzreihen

















































![{\displaystyle {\sqrt[{q}]{a^{p}}}=a^{\frac {p}{q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5f064b2b5c3a83176ec72959edc61a5c8347d5a)






























































![{\displaystyle [-0{,}4\,;\,0{,}4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f74042094692ac8b78800e0946dad319f884be10)




![{\displaystyle \exp(x)\in \left[e_{n}(x),E_{n}(x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc460e1554f5b967d22716f29cd0d196cb905c78)
























![{\displaystyle {\begin{aligned}\ell (x)&=E_{n}(x)-e_{n}(x)=\left(1-{\frac {x}{n}}\right)^{-n}-\left(1+{\frac {x}{n}}\right)^{n}\\&=\left(1-{\frac {x}{n}}\right)^{-n}\left[1-\left(1-{\frac {x}{n}}\right)^{n}\left(1+{\frac {x}{n}}\right)^{n}\right]\\&=\left(1-{\frac {x}{n}}\right)^{-n}\left[1-\left(1-{\frac {x^{2}}{n^{2}}}\right)^{n}\right]\\&=E_{n}(x)\left[1-b_{n}(x)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/452723b8aa083adc86fada788854404820fdcc71)















![{\displaystyle {\begin{aligned}\exp(x+y)=&\sum _{n=0}^{\infty }{\frac {(x+y)^{n}}{n!}}\\[0.3em]=&\sum _{n=0}^{\infty }{\frac {1}{n!}}\sum _{k=0}^{n}{\binom {n}{k}}x^{k}\cdot y^{n-k}\\[0.3em]=&\sum _{n=0}^{\infty }{\frac {1}{n!}}\sum _{k=0}^{n}{\frac {n!}{k!(n-k)!}}x^{k}\cdot y^{n-k}\\[0.3em]=&\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {x^{k}}{k!}}\cdot {\frac {y^{n-k}}{(n-k)!}}\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed11b04f7e2fae4229322fd38f3719a663070ca3)


![{\displaystyle {\begin{aligned}\exp(x)\cdot \exp(y)=&\left(\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right)\cdot \left(\sum _{n=0}^{\infty }{\frac {y^{n}}{n!}}\right)\\[0.3em]=&\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {x^{k}}{k!}}\cdot {\frac {y^{n-k}}{(n-k)!}}\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e6c6b711d528932f3ae03665d983e59bee5b06e)



![{\displaystyle \exp(x)=\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}=1+x+\underbrace {\sum _{k=1}^{\infty }{\frac {x^{2k}}{(2k+1)!}}[(2k+1)+x]} _{\geq 0\quad \forall x\geq -3}\geq 1+x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c26e6f604f2d0dafec14432e073ab311351f44a)






















































































