Diskussion:Multiplikation
Einleitungssatz[Quelltext bearbeiten]
Der Einleitungssatz laesst mich stutzen: Wie kann man bei der Multiplikation 1.3 * 3.14 "wiederholt addieren"? tsor 21:54, 8. Sep 2003 (CEST)
Hier fehlt nastürlich "im Bereich der natürlichen Zahlen" Genau das ist ja der Punkt, den ich schon wiederholt moniert habe. Das, was wiederholt wird, ist der Multiplikand; der Multiplikator ist die Anzahl der Additionen. Unstrittig ist m.E. auch, dass der Multiplikand dem 1. Faktor entspricht. Somit ist die Schreibweise 4•3= 4 + 4 + 4 korrekt und die angegebene Schreibweise falsch. JP 250853
- Hab ich schon erwaehnt, dass ich's ueberarbeitet hab? :) --SirJective 13:05, 11. Feb 2004 (CET)
Multiplikation mit den Fingern[Quelltext bearbeiten]
Habe einmal den Abschnitt Multiplikation mit den Fingern hinzugefügt. Mangels Digitalkamera, konnte ich leider keine guten Grafiken anfertigen, wollte jedoch irgendwie verständlich machen, was ich mit Worten auszudrücken nicht in der Lage war. Hoffe, dass man nun einigermaßen vesteht, wie as mit der Multiplikation funktioniert und dass jemand anders sich bereit erklärt, seine Finger zu photographieren. Ansonsten wäre ich auch ganz dankbar, wenn jemand die Formatierung übernimmt :P --Yuszuv 20:25, 3. Mär 2005 (CET)
Dieser Abschnitt ist derart unverständlich, dass er einer Überarbeitung bedarf!
April, 2007
Ich schließe mich der Meinung an, der Abschnitt sollte gelöscht werden. Begründung:
- Es wird ausgeführt, dass die Faktoren in der ersten Dekadenhälfte liegen müssen, dann heißt es aber, dass auch die 6 zulässig ist. Die 6 liegt m. E. in der zweiten Dekadenhälfte.
- Der Abschnitt verwirrt mehr und vernebelt das Verständnis für die Multiplikation, als dass er hilfreich wäre.
- Kindern kann man diese Erklärung nicht zumuten, dagegen erscheint die Addition mit den Händen sinnreich für Kinder.
--Mnntoino 12:49, 9. Apr. 2008 (CEST)
Da muss ein Fehler drin sein, da es bei der Multiplikation von 24 und 22 heißt, man solle 4*2 nehmen, an der linken Hand gibt es aber nur einen oberen Finger.
Ich glaube einen weiteren Fehler entdeckt zu haben. In der Beschreibung des ersten Falls steht: "(d-1) · 10 multipliziert, ...". Beim Beispiel unten wird dann mit 10 multipliziert, da die Dekade d = 1 ist. Ich bekomme da aber (d-1)·10 = (1-1)·10 = 0 · 10 = 0 heraus. Was der Autor gleich zwei Zeilen weiter unten wieder richtig macht: "Die additive Konstante (d-1) · d · 100 ist hier 0 · 1 · 100 = 0." --87.179.88.234 20:18, 22. Mär. 2010 (CET)
Multiplikation mit dem Abakus[Quelltext bearbeiten]
Weiß jemand, wie die Multiplikation mit dem Abakus funktioniert?
Multiplikation gleich Addition der Logarithmen, wie beim Rechenschieber.--62.225.152.1 6. Jul 2005 14:31 (CEST)
- Im Prinzip ist das gleiche wie schriftliches Multiplizieren, nur das man von links anfängt und es paar "Regeln" gibt, die man sich einprägen kann, wenn man nicht jedes Mal nachdenken muss, wie man die einzelnen Kugeln verschieben muss. Werde es demnächst vielleicht mal in den Artikel einpflegen --Yuszuv 6. Jul 2005 16:07 (CEST)
vedische / altindische Multiplikation[Quelltext bearbeiten]
Kann jemand das vedische Multiplikationsverfahren für große Zahlen kurz und verständlich erklären? Ich versteh nur die Beispiele für Zahlen kurz über oder unter der selben 10^n-Grenze (Bin bei diesen aber begeistert). Ich schaffe es nicht den Artikel „Ein ganzheitlicher Zugang zur kreativen Bildung durch altindische Mathematik - ein neues Beispiel“ wikipedia gerecht zusammenfassen. --Gruftelfe 19.08.05 14:22
Multiplikand und Multiplikator[Quelltext bearbeiten]
"a und b nennt man Faktoren oder Multiplikanden" - Soweit ich weiß, ist a der Multiplikator und b der Multiplikand,- das ist ein Unterschied! Der erstere ist "aktiv", der richtet sich auf den Multiplikanden, und der zweite ist "passiv", mit dem wird etwas getan. Benjamin Schreyer
rekursive Schreibweise[Quelltext bearbeiten]
macht es Sinn eine rekursive Schreibweise mit anzugeben? Habe hier einen kleinen Java Schnipsel grade geschrieben:
public static int rekursivMul(int a, int b){
if(a <= 1){
return b; //wenn am Ende der Rekursion, Ergebnis zurückgeben
}
else{
return (rekursivMul( a-1, b) +b); //rekursiver Aufruf
}
}
Bezieht sich aber eigentlich auch darauf, dass Multiplikation durch Addition ausgeführt wird...
- Ich halte das Beispiel nicht für sinnvoll. Erst einmal funktioniert es nur für Zahlen aus einem gewissen Bereich, d.h. "a" muss positiv sein (0 * b != b; ausser b=0) und ab bestimmten Werten bekommt man Integer-Overflows, die bei Pseudo-Code im Gegensatz zu Java nicht auftreten. Das Verfahren an sich ist zudem extrem ineffizient und auch nicht die Methode wie Computer multiplizieren. Da gab es vor 5000 Jahren schon bessere Verfahren. Der Code dient bestenfalls als einfaches Beispiel für Rekursion, aber auch da gibt es schönere und sinnvollere Beispiele. --82.141.61.150 15:12, 20. Mai 2007 (CEST)
Multiplikand vs. Multiplikator[Quelltext bearbeiten]
Sind in der Einleitung Multiplikand und Multiplikator vertauscht. Wenn ich b+b+b rechne, ist dann nicht b der Multiplikand und 3 der Multiplikator ? (nicht signierter Beitrag von 77.181.252.172 (Diskussion) 16:19, 19. Okt. 2007)
- Das sehe ich genauso. (nicht signierter Beitrag von 82.82.97.40 (Diskussion) 15:51, 28. Apr. 2009 (CEST))
- Die Frage ist aber, ob das dann 3 · b oder b · 3 ist. --Digamma (Diskussion) 19:23, 16. Dez. 2015 (CET)
- Der "Bartsch - Taschenbuch Mathematischer Formeln" sieht das ebenfalls so. Ein weiteres Argument ist, um mit der Division in Einklang zu bleiben (Dividend geteilt durch den Divisor ergibt den Quotienten) sollte auch hier die Reihenfolge, Multiplikand mal Multiplikator ergibt das Produkt, gewählt werden. Und schließlich das Argument von der Herkunft der unterschiedlichen Namen (eigentlich sind beides Faktoren und damit austauschbar). Die Multiplikation als glorifizierte Multiplikation. Zum Beispiel 2 · 3, hier wird eine Menge mit der Anzahl 2 (zum Beispiel Äpfel ;) {Apfel, Apfel} zu Grunde gelegt und diese in einer Menge von Drei betrachtet ({{Apfel, Apfel},{Apfel, Apfel},{Apfel, Apfel}}). Die zu Grunde gelegte Menge ist der Multiplikant, die übergeordnete betrachtete Menge ist der Multiplikator. Die Auslegung Multiplikand · Multiplikator kommt imho aus dem alltäglichen Sprachgebrauch 2 · 3, man hat zwei mal die Drei. Und nicht aus dem mehr logischen von links nach rechts aufgebauten Ansatz, 2 · 3 die Menge 2 kommt drei mal vor. Wie ich sehe, hat diese Diskussion schon vor über zehn Jahren begonnen. Sind denn die Argumente für Multiplikand · Multiplikator nicht schlagkräftig genug (einschließlich des Bartsch)? Oder haben wir (einschließlich des Bartsch) unrecht? Oder interessiert sich einfach niemand dafür diesen Artikel zu korrigieren? Ich bin auf diese Diskussion gestoßen, weil meine Tochter nun sogar schon in der Schule die imho unlogische Version Multiplikator · Multiplikand beigebracht bekommt. --Torojima (Diskussion) 11:42, 30. Sep. 2018 (CEST)
- Was ist an 3 (Multiplikator) Äpfeln (Multiklikand) unlogisch? Oder habe ich dich dich irgendwo falsch verstanden? --Fritzbruno (Diskussion) 18:01, 30. Sep. 2018 (CEST)
Ich habe auch gelernt: Multiplikant x Multiplikator = Produkt siehe auch https://de.wikipedia.org/wiki/Grundrechenart - Da widerspricht sich Wikipedia selbst (nicht signierter Beitrag von Udo-paul (Diskussion | Beiträge) 15:46, 11. Mai 2020 (CEST))
- Was, glaube ich klar ist: Wenn man die Multiplikation als wiederholte Addition auffasst, dann ist das, was wiederholt addiert wird, der Multiplikand (mit d!) und die Anzahl, wie oft es addiert wird, der Multiplikator. Ob man jetzt aber 2·3 als 2 + 2 + 2 oder als 3 + 3 auffasst, ist nicht klar. Bei dem Beispiel mit den 3 Äpfeln, oder wenn das eine eine Größe mit Einheit und das andere eine reine Zahl ist, ist es klar. Im Allgemeinen aber nicht. Und wenn man zum Beispiel einen Flächeninhalt berechnet, macht es inhaltlich keinen Sinn, zwischen Multiplikand und Multiplikator zu unterscheiden. --Digamma (Diskussion) 15:58, 11. Mai 2020 (CEST)
Multikplikation nicht abgeleitet von der Addition ?[Quelltext bearbeiten]
Am Anfang des Artikels wird ausgeführt, dass die Multiplikation das Hintereinanderausführen der Addition ist. Weiter wird ausgeführt, dass die Multiplikation in den Strukturen der Körper und Ringe eine eigene Operation darstellt. Der Operator kann allgemein also nicht von der Addition abgeleitet werden. Wer kann diesen Widerspruch auflösen?--Mnntoino 16:05, 2. Jan. 2011 (CET)
Algorithmen zum Multiplizieren[Quelltext bearbeiten]
Im Artikel fehlen noch die verschieden Algorithmen zur Multiplikation mit Zettel und Stift, also die Variante die in Deutschland gelehrt werden und die Varianten die im Angel Sächsischen Raum gelehrt werden (Das sind nämlich andere, die in den en: Math wars teilweise stark diskutiert werden). Wenn man das auch für Schüler verständlich schreiben will, ist das schon einiger Aufwand, wofür ich im Moment leider keine Zeit habe. Schönen Gruß "Wohingenau" 11:38, 9. Nov. 2008 (CET)
Schriftliche Multiplikation[Quelltext bearbeiten]
Ich finde es sehr irritierend, dass in dem Artikel nichts zur klassischen schriftlichen Multiplikation (wie sie in Schulen unterrichtet wird) steht. Martinwilke1980 08:38, 11. Aug. 2011 (CEST)
- Hier steht das. Aber du hast völlig Recht, es müsste darauf eingegangen werden, wie das in der Schule gemacht wird (wie in Schriftliche Addition) und wie das mit dem dort beschriebenen Algorithmus zusammenhängt. --Chricho ¹ ² 01:36, 2. Apr. 2012 (CEST)
- Hier steht das.
- Das ist aber für all jene, die die Summenschreibweise nicht kennen, völlig unverständlich. Und das trifft nach meiner Einschätzung auf alle zu, die die Schule nach der 10. Klasse verlassen haben. Und wenn man darauf eingehen sollte, wieso hat das dann eigentlich noch niemand getan? --84.60.97.43 00:06, 4. Jul. 2015 (CEST)
Erledigt --RolandIllig (Diskussion) 16:13, 15. Dez. 2018 (CET)
Namensgebung Multiplikation[Quelltext bearbeiten]
Zur Person: Majo250853
StD; Seminarlehrer für Mathematik in Bayern seit 1997; Studium der Fächer Mathematik und Physik an der TU München in den Jahren 1972 bis 1977 Mein Änderungsvorschlag zum Artikel wurde leider verworfen; die geänderte Fassung enthält m.E. aber zwei grobe Fehler. Hierzu einige Anmerkungen. Die Frage, ob 3*4 als 3 + 3 + 3 +3 oder als 4 + 4 + 4 zu interpretieren ist, wird in der didkatischen Literatur seit langer Zeit sehr kontrovers und emotional diskutiert. Die Frage scheint zunächst unbedeutend, jedoch gibt es durchaus Problemstellungen, bei denen die Reihenfolge der Faktoren eine Rolle spielt, z.B. bei der Multplikation einer Größe mit einer Zahl und bei Algorithemen in der numerischen Mathematik und der Informatik. Im Elementaunterricht kommt die Frage zum tragen, wenn zur Veranschaulichung Größen multipliziert werden. Ist die Schreibweise 3 kg * 4 oder 4 * 3 kg zweckmäßig. Rein semantisch würde man eher zur zweiten Schreibweise tendieren; von der Fachsystematik her spricht allerdings viel für die Variante 1.
Walther Lietzman hat in der zweiten Auflage seiner Methodik des Mathematikunterrichts auf die Empfehlung der DAMNU für die erste Schreibweise hingwiesen und sinngemäß gefordert, dass die Schulen dieser Empfehlung folgen sollten.
Für die Schreibweise 3kg * 4 spricht m. E. folgendes;
1. Die Schreibweise ist analog zur Division gebildet. 9 kg : 3 ist sinnvoll, 9 : 3 kg müßte als (9 : 3) kg interpetiert werden, im krassen Gegensatz zur Schreibweise in der Physik.
2. Die gängige Berechnugen von zusammengesetzten Bruchteilen erfolgt so: 3/4 von 40 kg = (40 kg : 4) * 3. Niemanden würde es einfallen, hier etwa folgendes aufzuschreiben: 3/4 von 40 kg = 3 * (40 kg : 4) Man kann diese Bruchteilregel zwar zur zweiten Schreibweise kompatibel gestalten, aber das wirkt dann schon sehr gekünstelt.
3. Bei der Division einer Größe durch eine Zahl bezeichnet der Divisor stets die unbenannte Zahl. Etwa bei 3kg : 6 ist 6 der Divisor. Analog sollte auch bei der Multiplikation der Multiplikator die unbenannte Zahl bezeichnen. (Wird auch bei Walther Lietzman ausführlich erörtert.)
4. Das Zurückführen der Division auf die Multiplikation mit dem Inversen (Kehrbruch) ist mit Schreibweise 2 nur schwer zu realisieren: 4kg : 2 = 4kg * 1/2 = 1/2 von 4 kg.(Nicht: 1/2 * 4kg!) Die Schreibweise 4 kg : 2 = 1/2 * 4kg würde den häufigen Schülerfehelr, von der falschen Zahl den Kehrbruch zu nehmen, weiter unterstüzten, da man wohl weiterhin 4:2 = 4 * 1/2 schreiben wird, wenn keine größe im Spiel ist. Schließlich gilt auch 3/4 von 4/5 = (4/5 : 4)*3 = 4/5 * 3/4. Letzteres ist aber eher unwichtig, da man meistdie Kommutativität der Multiplikation ins Zentrum rückt und die Multiplikation von Brüchen mit geometrischen Veranschaulichungen herleitet
5,Völlig unstrittig ist m.E.die die Begriffsbildung Multiplikand * Multiplikator ; wird auch in der Informatik so benannt. (Vergleiche den Wikipedia Artikel zum Booth-Algorithmus). Solche Erläuterungen wären völlig unverständlich, wenn man die Reihenfolge von Multiplkand und Multiplkator beim Produkt einfach vertauschen dürfte. Diese Schreibweise ist nicht kommuntativ, man darf also nicht einfach Multiplikator * Multiplikand schreiben. Völlig abwegig in dem Artikel erscheint mir die Ansicht, dass je nachdem, auf welcher Seite des "=" - Zeichens der Ausdruck "Wert des Produktes" steht, die Reihenfolge der Namen der Glieder des Produktes geändert wird. Logischerweise hat bei einem Produktterm aus zwei Gliedern jedes Glied einen eigenen, fest definierten Namen. Die Begriffe Multiplikand und Multiplikator stehen ja als Synonyme für 1. Faktor und 2. Faktor. Hier würde niemanden einfallen, die Reihenfolge zu vertauschen. --Majo250853 12:32, 11. Okt. 2011 (CEST)
- Die Einwände sind auch zehn Jahre später immer noch sehr berechtigt. Es ist keineswegs selbstverständlich, daß die Multiplikation kommutativ ist, und i. a. ist sie das auch nicht, obwohl das für manche Zahlenkörper wie z. B. die reellen und komplexen Zahlen sowie Teilkörper davon - eher zufällig - zutrifft. Der naive Zugang zur Multiplikation geht von der Aufgabenstellung aus, einen Algorithmus zu finden, der zu einer natürlichen Zahl, dem Multiplikanden, ein nicht-negatives ganzzahliges Vielfaches bildet, wobei die Vielfachheit Multiplikator genannt wird. Den Term a*b kann man auf zwei Arten lesen: 1. "a mal b" - das bedeutet semantisch, daß der Multiplikand b ver-a-facht, also a-mal genommen werden soll; a ist dann offensichtlich der Multiplikator. 2. "a multipliziert mit b" - in dieser Lesart sind offensichtlich a der Multiplikand und b der Multiplikator. Die "naive" Multiplikationsmethode ist natürlich, den Multiplikanden einmal weniger, als der Multiplikator angibt, zum Multiplikanden zu addieren. Daß die Operation unter relativ vielen Umständen kommutativ ist, wird in dieser Sicht zunächst einmal überhaupt nicht deutlich und wird zwar durch die Rechteckanordnung von Zähltokens oder die Darstellung des Produkts als Flächeninhalt eines Rechtecks suggeriert, aber in den unteren Jahrgangsstufen natürlich nicht bewiesen. Auch der übliche Schulalgoritmus der schriftlichen Multiplikation unterscheidet klar zwischen Multiplikator und Multiplikandem, und die Rechnung sieht trotz gleichem Ergebnis der Zeilensummation vollkommen anders aus, wenn die beiden Faktoren vertauscht werden. Völlig verwirrend ist die Flächeninhaltsdarstellung, weil dabei eine Dimensionsänderung stattfindet. Im Gegensatz zu Zahlen sind Strecken nicht dimensionslos, sondern Größen mit der Einheit "Längeneinheit". Wenn man zwei Strecken miteinander multipliziert, dann ist das Produkt eine Größe mit der Einheit "Flächeneinheit"; das ist etwas völlig anderes als die Vervielfachung einer Streckenlänge durch Multiplikation mit einer Zahl. Jedenfalls ist es nicht gerechtfertigt, "ex cathedra" den einen Teilausdruck des Terms a*b als Multiplikand bzw. Multiplikator zu definieren, und es ist auch eine faule Ausrede, sich dabei dann auf die Kommutativität zu berufen und das Problem damit wegzudefinieren. Vielmehr ist es zwingend erforderlich, sich damit im Zusammenhang mit der Namensgebung inhaltlich auseinanderzusetzen. --95.112.90.145 07:25, 21. Feb. 2021 (CET)
- Was heißt das jetzt für den Artikel? --Digamma (Diskussion) 12:08, 21. Feb. 2021 (CET)
- Daß die Feststellung, daß a der Multiplikator ist, in dieser Allgemeinheit falsch ist und durch eine Darstellung des wahren, verwickelteren Sachverhalts ersetzt werden muß. --95.112.90.145 16:52, 21. Feb. 2021 (CET)
- Einverstanden. Du kannst dich gerne daran versuchen. --Digamma (Diskussion) 20:43, 21. Feb. 2021 (CET)
- Ich hätte mich beinahe tatsächlich darangemacht. Bis mir dann klar wurde, daß das eigentlich ziemlicher Unfug und Befassung mit einem Scheinproblem bzw. einer "didaktischen Fragestellung" ist: Die Definition von "Multiplikand" und "Multiplikator" bzw. deren Unterscheidung ist nur sinnvoll bei zweistelligen Multiplikationstermen auf der Menge der natürlichen Zahlen, und natürliche Zahlen kommen im wahren Leben praktisch nicht vor, da hat man es im allgemeinen mit Größen oder, gewöhnlich reellen, Skalaren zu tun. (Veranschaulichung: was in (4/3)*Pi*-e*(1+i) soll denn ein Multiplikand oder ein Multiplikator sein?) Ich denke, bevor man sich mit solchen Feinheiten überhaupt befaßt, sollten die im Abschnitt "Inhalt des Lemmas" angesprochenen Fragen geklärt werden. --77.0.188.221 07:18, 22. Feb. 2021 (CET)
- Einverstanden. Du kannst dich gerne daran versuchen. --Digamma (Diskussion) 20:43, 21. Feb. 2021 (CET)
- Daß die Feststellung, daß a der Multiplikator ist, in dieser Allgemeinheit falsch ist und durch eine Darstellung des wahren, verwickelteren Sachverhalts ersetzt werden muß. --95.112.90.145 16:52, 21. Feb. 2021 (CET)
- Was heißt das jetzt für den Artikel? --Digamma (Diskussion) 12:08, 21. Feb. 2021 (CET)
Asiatische, chinesische oder japanische Multiplikation[Quelltext bearbeiten]
Im Artikel fehlt das graphische Verfahren, das als asiatische, chinesische oder japanische Multiplikation bezeichnet wird. --Rôtkæppchen68 22:50, 20. Jan. 2013 (CET)
- Danach hab ich auch gerade gesucht. Solche Artikel mit abstrakten Zeichen und Formeln schrecken mich immer etwas ab. Vielleicht ist "vedisch" nur ein Synonym für "indisch", was Google neben "chinesischer Multiplikation" als Suchbegriff vorschlägt? Aber eigentlich komm ich gerade von einer Seite, die die "jap. Multiplikation" erklärt: https://www.genialetricks.de/japan-trick/ Es kommt mir so vor, als ob der Trick mit den Essstäbchen schon mal Gegenstand einer TV-Quizfrage war, vermutlich bei "Wer weiß denn sowas?". 46.114.140.152 11:32, 22. Okt. 2020 (CEST)
Ersetzt "ein nicht gesetzter Malpunkt" eine Klammer?[Quelltext bearbeiten]
Beispiel 1:
6:2(2+1)
ist entweder =9 oder =1
Beispiel 2:
a:2a
ist entweder =a*a/2 oder =1/2
Selbst wissenschaftliche Taschenrechner kommen hier zu unterschiedlichen Ergebnissen.
Folgende Fragen ergeben sich:
Ersetzt "ein nicht gesetzter Malpunkt" eine Klammer? Sind * und : gleichwertig? Wenn keine Klammern gesetzt sind, werden dann Ausdrücke ausschließlich von links nach rechts abgearbeitet? Ist der Ausdruck a:2a der gleiche wie a:2*a
Es gibt weder in Bronstein noch im Kusch eine Antwort auf diese Fragen.
Wiki sollte hier eine Antwort geben können im Kapitel Division oder Multiplikation. (nicht signierter Beitrag von 88.73.23.211 (Diskussion) 23:52, 29. Nov. 2014 (CET))
- Der Doppelpunkt ist nur eine minderwertige Ersatzdarstellung für den Bruchstrich. Um alle Ambiguitäten zu vermeiden, schreibst Du Deinen Ausdruck mit Bruchstrich. Je nachdem, ob Du , , oder schreibst, kommt eben etwas anderes dabei heraus. Die Division ist nicht kommutativ oder assoziativ. --Rôtkæppchen₆₈ 00:01, 30. Nov. 2014 (CET)
Es stimmt, wenn man in den beiden Beispielen einen Bruchstrich verwendet wird die Sache eindeutig. Ebenso wird die Sache eindeutig, wenn man zusätzliche Klammern verwendet. Es sollte doch aber in der Mathematik auch eine eindeutige Rechtsprechung geben, wie zu verfahren ist, wenn die Ausdrücke genau so aufgeschrieben sind, wie in den beiden obigen Beispielen. Es sind schließlich kurze und einfache Ausdrücke und ich habe noch nicht gehört, dass diese Schreibweise verboten wäre. (nicht signierter Beitrag von 88.73.3.250 (Diskussion) 22:15, 5. Dez. 2014 (CET))
Namensgebung: Ergebnis einer Multiplikation "Produkt" oder "Produktwert"?[Quelltext bearbeiten]
|
- - - - Wer ein ein vorläufiges Ergebnis dieser Diskussion sehen will, der scrolle runter auf die Aussagen von Benutzer Digamma mit den Zeitstempel "10:41, 20. Dez. 2015". --Stefan B. Link (Diskussion) 09:00, 25. Dez. 2015 (CET) |
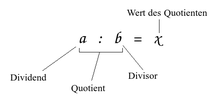
--Stefan B. Link (Diskussion) 08:20, 10. Dez. 2015 (CET) schreibt: Im Artikel "Division" wird die Operation einer Divion "Quotient" genannt, das Ergebnis jedoch "Wert des Quotienten". Siehe hier:
- Dabei heißen:
- Die Zahl , die geteilt wird, „Dividend“ (lateinisch das zu Teilende), in der Bruchrechnung auch „Zähler“.
- Die Zahl , durch die geteilt wird, „Divisor“ (lateinisch der, der teilt), in der Bruchrechnung auch „Nenner“.
- Der Term heißt „Quotient“.
- Das Ergebnis der Division heißt „Wert des Quotienten“ oder Quotientenwert, häufig kurz auch Quotient.
- Dabei heißen:
Auch hier müsste es doch analog heißen:

- Der Term heißt „Produkt“.
- Das Ergebnis der Multiplikation heißt "Wert des Produktes" oder Produktwert, häufig kurz auch Produkt.Adresse
Wie nennt man denn die Aussage "a*b"? Man nennt dies doch nicht "Multiplikator * Multiplikand", sondern man nennt dies "Produkt". Oder hat - unsinner Weise - die Aussage "a * b" gar keinen Namen - wobei nur das Äquivalent dann "Produkt" hieße?--Stefan B. Link (Diskussion) 08:20, 10. Dez. 2015 (CET)
- - - - -
Auch im Artikel "Subtraktion" heißt es im 4. Aufzählungspunkt:
- Das Ergebnis einer Subtraktion ist der Wert der Differenz (auch Differenzwert oder auch kurz nur Differenz).
Heute, bis zum 14.12.2015, fehlt nur die entsprechende Grafik. Ich will dieses Fehlen morgen zunächst in der Diskussion anführen.--Stefan B. Link (Diskussion) 06:34, 14. Dez. 2015 (CET)
- kann es sein, dass bei dieser Diskussion bislang von der Grundschulrechenart ausgegangen wird? Der Begriff Wert des Produkts wird spätestens beim Vektorprodukt sinnlos, denn was ist hier der Wert? Auch bei der Multiplikation (aber auch anderer Verknüpfungen) komplexer Zahlen ist der Begriff Wert kaum zu gebrauchen. --Fritzbruno (Diskussion) 17:55, 14. Dez. 2015 (CET)
- --Stefan B. Link (Diskussion) 05:55, 16. Dez. 2015 (CET) schreibt: Lieber Fritzbruno, wie es im Lemma steht, geht es hier im Artikel um "eine der vier Grundrechenarten in der Arithmetik". Mit dem Vektorprodukt gibt es wohl Ähnlichkeiten, aber auch Unterschiede - die so groß sein dürften, dass in einem Falle zu Recht vom "Wert des Produktes" gesprochen werden kann und im anderen Falle nicht. Ob man das aber 1. so sehen kann und wie 2. meine Sichtweise argumentativ zu begründen wäre, weiß ich nicht zu sagen, da ich kein Mathematiker bin. Ich will hier die Diskussion zwischen Fachleuten anregen, denn schon öfter las ich in mathematischen Bücher, dass zwischen den Termen einer Summe, eines Produktes, einer Differenz und eines Quotienten worthaft unterschieden wird von deren Ergebnissen - eben als "Wert einer Summe, eines Produktes, einer Differenz oder eines Qutotienten". Logisch ist der Term einer mathematischen Aussage etwas anderes als ihr Ergebnis. Und deswegen - ob der begrifflichen Eindeutigkeit willen - müsste der Term anders benannt werden als sein Ergebnis. Z. B. sollte der Term "Quotient" heißen, das Ergebnis aber "Wert des Quotienten" - nur kurz gesprochen nennt man das Ergebnis auch "Quotient", wobei wir bei der Namensgebung wären, die ich im 5. Schuljahr lernte und die logisch deshalb falsch ist, weil zwischen einem Term und seinem Ergebnis als zwei unterschiedlichen Dingen zu reden ist. Aber heute gibt es didaktische Mathe-Literatur, die vom "Wert eines Quotienten" als dem Ergebnis eines Quotienten sprechen - logisch richtigerweise so sprechen. Mag sein, dass mein logischer Blick anderes ausfiele bzw. und ich keine Unterschiede sähe zwischen einem Quotienten und seinem Ergebnis und deswegen beides "Quotient" hieße, wenn mein Mathe-Wissen komplexer wäre.--Stefan B. Link (Diskussion) 05:55, 16. Dez. 2015 (CET)
- Nun, wenn Logik gefragt ist: mathematisch gesehen gibt es kein "Ergebnis" einer Gleichung. Die mathematische Logik unterscheidet nicht zwischen der linken und der rechten Seite einer Gleichung, wenn also die linke Seite ein Produkt (eine Summe, eine Differenz, einen Quotienten, eine Wurzel, ...) darstellt, dann auch die rechte. --Fritzbruno (Diskussion) 18:43, 16. Dez. 2015 (CET)
- --Stefan B. Link (Diskussion) 05:55, 16. Dez. 2015 (CET) schreibt: Lieber Fritzbruno, wie es im Lemma steht, geht es hier im Artikel um "eine der vier Grundrechenarten in der Arithmetik". Mit dem Vektorprodukt gibt es wohl Ähnlichkeiten, aber auch Unterschiede - die so groß sein dürften, dass in einem Falle zu Recht vom "Wert des Produktes" gesprochen werden kann und im anderen Falle nicht. Ob man das aber 1. so sehen kann und wie 2. meine Sichtweise argumentativ zu begründen wäre, weiß ich nicht zu sagen, da ich kein Mathematiker bin. Ich will hier die Diskussion zwischen Fachleuten anregen, denn schon öfter las ich in mathematischen Bücher, dass zwischen den Termen einer Summe, eines Produktes, einer Differenz und eines Quotienten worthaft unterschieden wird von deren Ergebnissen - eben als "Wert einer Summe, eines Produktes, einer Differenz oder eines Qutotienten". Logisch ist der Term einer mathematischen Aussage etwas anderes als ihr Ergebnis. Und deswegen - ob der begrifflichen Eindeutigkeit willen - müsste der Term anders benannt werden als sein Ergebnis. Z. B. sollte der Term "Quotient" heißen, das Ergebnis aber "Wert des Quotienten" - nur kurz gesprochen nennt man das Ergebnis auch "Quotient", wobei wir bei der Namensgebung wären, die ich im 5. Schuljahr lernte und die logisch deshalb falsch ist, weil zwischen einem Term und seinem Ergebnis als zwei unterschiedlichen Dingen zu reden ist. Aber heute gibt es didaktische Mathe-Literatur, die vom "Wert eines Quotienten" als dem Ergebnis eines Quotienten sprechen - logisch richtigerweise so sprechen. Mag sein, dass mein logischer Blick anderes ausfiele bzw. und ich keine Unterschiede sähe zwischen einem Quotienten und seinem Ergebnis und deswegen beides "Quotient" hieße, wenn mein Mathe-Wissen komplexer wäre.--Stefan B. Link (Diskussion) 05:55, 16. Dez. 2015 (CET)
- Es geht auch nicht um das "Ergebnis einer Gleichung", sondern um das Ergebnis einer Rechenoperation bzw. den (Funktions-)Wert einer 2-stelligen Funktion bzw. Wert eines Terms. --Digamma (Diskussion) 19:21, 16. Dez. 2015 (CET)
- Ok, was ist der Wert der Rechenoperation (2i+7)*(5+3i)? Es ist schwer, bei komplexen Zahlen, die nun mal nur einen Betrag, aber keinen "Wert" haben, einen "Wert des Produkts" anzugeben. Oder gibt es einen eigenen Artikel Multiplikation komplexer Zahlen und dieser hier beschränkt sich allein auf reelle? --Fritzbruno (Diskussion) 19:55, 17. Dez. 2015 (CET)
- Der Wert ist die komplexe Zahl 29 + 31i. Die komplexe Zahl "hat" keinen Wert, sie "ist" der Wert des Terms (2i+7)*(5+3i). Als "Wert" wird in der Mathematik jedes Ergebnis einer Rechenoperation bzw. jedes Bildelement einer Abbildung bzw. Funktion bezeichnet, völlig unabhängig davon, ob es sich um eine Zahl oder ein anderes Objekt handelt. Auch ein Vektor kann ein Funktionswert sein. --Digamma (Diskussion) 20:44, 17. Dez. 2015 (CET)
- - - - Die Diskussion hierzu nimmt Benutzer Digamma besser erklärend weiter unten nochmals auf im Abschnitt mit dem Zeitstempel 10:41, 20. Dez. 2015.--Stefan B. Link (Diskussion) 13:02, 23. Dez. 2015 (CET)
- @ Fritzbruno / Aussagenlogisch betrachtet (und die Mathematik produziert sehr wohl Aussagen) gibt es einen Unterschied zwischen der Aussage "Hans ist der Bruder von Inge" = "Sie sind Geschwister." "Geschwister" ist nicht identisch ("synonym") mit Bruder, denn "Geschwister" könnte auch bedeuten "x Schwester von y". Geschwister ist eine abstraktere Zusammenfassung der Aussage vor dem "ist/sind". Nun analog: "2+2" "=4". Die Anzahl (Zahl) von vier, die mit der Ziffer "4" bezeichnet wird, ist keine Summe, sondern eine genau definiete Menge. Eine Summe von "4" ist genau definiert "1+1+1+1" oder "2+1+1". Mit "1+1+1+1" wird ausgesagt, dass z. B. jemand 1 Menge hat, dann noch 1 Menge dazuerhält usw. Mit "2+1+1" wird ausgesagt, dass eine Menge von "2" vorliegt, und dazu noch 1 Menge kommt, und zeitlich undefiniert noch eine Menge der Anzahl eins dazukommt. "4" ist eine für sich stehende Menge, die etwas anderes darstellt (konkret bezeichnet) als z. B. eine Summe von 4 Mengen. Mathematische Aussagen sind keine eigene Aussagenform, die außerhalb der Aussagenlogik lägen. Mathematik ist eine abstrakte Struktur von unterschiedlichen Fällen. Ob mit der Aussage "4" jener oder ein anderer Fall ausgedrückt wird, spielt, abstrakt gesehen, keine Rolle. Und ist nicht das der Grund, warum viele etwas links der Gleichung genauso wie die Aussage rechts des Gleichheitszeichens benennen? Und müsste man nicht deshalb, um genau zu sprechen, die Aussage rechts der Gleichung mit "Wert + Genitivkonstruktion des Art-Termes links des Gleichheitszeichens benennen" - so wie das heute in mancher mathematischen Literatur ausgesagt wird? Es mag sein, dass ich Unsinn rede, denn ich fasse zusammen, was ich so gelesen und so verstanden habe, wobei "ich" hier mitbedeutet: "Kein studierter Mathematiker".--Stefan B. Link (Diskussion) 09:21, 17. Dez. 2015 (CET)
- Deine Terminologie lässt sehr zu wünschen übrig. Mit Mengen im Sinne der Mathematik hat der hier diskutierte Sachverhalt nichts zu tun. --Rôtkæppchen₆₈ 09:28, 17. Dez. 2015 (CET)
- Dem kann ich nur zustimmen! --Fritzbruno (Diskussion) 19:55, 17. Dez. 2015 (CET)
- Gut, dann argumentiere ich anders. "5 + 7 = 12 = 15 - 3" Frage: Ist "12" bei dieser Ausagenfolge eine Summe oder eine Differenz? Entweder - oder, beides geht nicht aufgrund des logischen Nichtwiderspruchsprinzips. Und lässt sich ein solcher Widerspruch (nicht im Wert!) in der Terminologie nur dadurch vermeiden, dass man "12" verschiedenen Rücksichten zuordnet? Einmal ist "12" der Wert einer Summe, andermal ist "12" der Wert einer Differenz. Bezeichnungen in der Mathematik sollten auch widerspruchfrei sein - konsitent für alle Aussagen sein, auch für Aussagen der Metasprache der Bezeichnung von mathematischen Elementen bei mathematischen Operationen.--Stefan B. Link (Diskussion) 06:23, 18. Dez. 2015 (CET)
- Selbstverständlich ist die 12 in Deinem Beispiel beides, denn ist ja nur kurz für . --Rôtkæppchen₆₈ 07:08, 18. Dez. 2015 (CET)
- Hast Recht, akzeptiert. Einmal ist deiner Meinung nach dann "12" eine Summe, andermal ist "12" ein Quotient. Dem steht jetzt noch die Aussage von Diagamma vom 17. Dez., 20:44 Uhr entgegen. --Stefan B. Link (Diskussion) 12:02, 18. Dez. 2015 (CET)
- Wenn man eine Zahl von einer anderen abzieht, bildet man eine Differenz. Ein Quotient wird gebildet, indem man eine Zahl durch eine andere teilt. --Rôtkæppchen₆₈ 13:57, 18. Dez. 2015 (CET)
- Hast Recht, akzeptiert. Einmal ist deiner Meinung nach dann "12" eine Summe, andermal ist "12" ein Quotient. Dem steht jetzt noch die Aussage von Diagamma vom 17. Dez., 20:44 Uhr entgegen. --Stefan B. Link (Diskussion) 12:02, 18. Dez. 2015 (CET)
- Selbstverständlich ist die 12 in Deinem Beispiel beides, denn ist ja nur kurz für . --Rôtkæppchen₆₈ 07:08, 18. Dez. 2015 (CET)
- Gut, dann argumentiere ich anders. "5 + 7 = 12 = 15 - 3" Frage: Ist "12" bei dieser Ausagenfolge eine Summe oder eine Differenz? Entweder - oder, beides geht nicht aufgrund des logischen Nichtwiderspruchsprinzips. Und lässt sich ein solcher Widerspruch (nicht im Wert!) in der Terminologie nur dadurch vermeiden, dass man "12" verschiedenen Rücksichten zuordnet? Einmal ist "12" der Wert einer Summe, andermal ist "12" der Wert einer Differenz. Bezeichnungen in der Mathematik sollten auch widerspruchfrei sein - konsitent für alle Aussagen sein, auch für Aussagen der Metasprache der Bezeichnung von mathematischen Elementen bei mathematischen Operationen.--Stefan B. Link (Diskussion) 06:23, 18. Dez. 2015 (CET)
- Dem kann ich nur zustimmen! --Fritzbruno (Diskussion) 19:55, 17. Dez. 2015 (CET)
- Deine Terminologie lässt sehr zu wünschen übrig. Mit Mengen im Sinne der Mathematik hat der hier diskutierte Sachverhalt nichts zu tun. --Rôtkæppchen₆₈ 09:28, 17. Dez. 2015 (CET)
- @ Fritzbruno / Aussagenlogisch betrachtet (und die Mathematik produziert sehr wohl Aussagen) gibt es einen Unterschied zwischen der Aussage "Hans ist der Bruder von Inge" = "Sie sind Geschwister." "Geschwister" ist nicht identisch ("synonym") mit Bruder, denn "Geschwister" könnte auch bedeuten "x Schwester von y". Geschwister ist eine abstraktere Zusammenfassung der Aussage vor dem "ist/sind". Nun analog: "2+2" "=4". Die Anzahl (Zahl) von vier, die mit der Ziffer "4" bezeichnet wird, ist keine Summe, sondern eine genau definiete Menge. Eine Summe von "4" ist genau definiert "1+1+1+1" oder "2+1+1". Mit "1+1+1+1" wird ausgesagt, dass z. B. jemand 1 Menge hat, dann noch 1 Menge dazuerhält usw. Mit "2+1+1" wird ausgesagt, dass eine Menge von "2" vorliegt, und dazu noch 1 Menge kommt, und zeitlich undefiniert noch eine Menge der Anzahl eins dazukommt. "4" ist eine für sich stehende Menge, die etwas anderes darstellt (konkret bezeichnet) als z. B. eine Summe von 4 Mengen. Mathematische Aussagen sind keine eigene Aussagenform, die außerhalb der Aussagenlogik lägen. Mathematik ist eine abstrakte Struktur von unterschiedlichen Fällen. Ob mit der Aussage "4" jener oder ein anderer Fall ausgedrückt wird, spielt, abstrakt gesehen, keine Rolle. Und ist nicht das der Grund, warum viele etwas links der Gleichung genauso wie die Aussage rechts des Gleichheitszeichens benennen? Und müsste man nicht deshalb, um genau zu sprechen, die Aussage rechts der Gleichung mit "Wert + Genitivkonstruktion des Art-Termes links des Gleichheitszeichens benennen" - so wie das heute in mancher mathematischen Literatur ausgesagt wird? Es mag sein, dass ich Unsinn rede, denn ich fasse zusammen, was ich so gelesen und so verstanden habe, wobei "ich" hier mitbedeutet: "Kein studierter Mathematiker".--Stefan B. Link (Diskussion) 09:21, 17. Dez. 2015 (CET)
- Hast Recht, Rotkäppchen; hab ich falsch benannt. Ich korrigiere: Einmal ist deiner Meinung nach dann "12" eine Summe, andermal ist "12" eine Differenz. Ich fahre fort:
- Du meinst, beim Differenzterm "15 - 3" ist/beträgt die Differenz "12"
- Statt "Differenzterm" kann man auch kurz "Differenz" sagen. Und kurz gesagt ist/beträgt "12" die Differenz (des Differenzterms, der, wie gerade gesagt, auch kurz "Differenz" genannt wird).
- Und du meinst dann richtigerweise (nach diesen Definitions-Prämissen), dass man dies grafisch so darstellen kann:
- .
- .
- Du meinst, beim Differenzterm "15 - 3" ist/beträgt die Differenz "12"
- Stimmt das? Habe ich dich da jetzt richtig verstanden?--Stefan B. Link (Diskussion) 09:21, 20. Dez. 2015 (CET)
- Hast Recht, Rotkäppchen; hab ich falsch benannt. Ich korrigiere: Einmal ist deiner Meinung nach dann "12" eine Summe, andermal ist "12" eine Differenz. Ich fahre fort:
- Das Ganze ist ein sprachliches Problem, deshalb lässt es sich auch nicht so einfach grafisch an der Formel darstellen:
- Man kann nicht sagen "12 ist eine Differenz". Zumindest ergibt das wenig Sinn, weil man jede Zahl als Differenz von zwei andern Zahlen darstellen kann. Es macht nur Sinn zu sagen "12 ist die Differenz von 15 und 3". Das Ergebnis einer Subtraktion ist also nie einfach nur eine Differenz, sondern immer die Differenz von Minuend und Subtrahend.
- Hingegen ist der Term "15 - 3" einfach eine Differenz. Der Wert dieses Terms ist das Ergebnis der Subtraktion, die Differenz von 15 und 3.
- Insofern heißt also sowohl der Term als auch das Ergebnis "Differenz", aber nur der Term ist eine Differenz "an sich", das Ergebnis ist immer nur die Differenz "von ... und ...". --Digamma (Diskussion) 10:41, 20. Dez. 2015 (CET)
- Also das ist doch mal Klarheit! Erstmals sehe ich keinen Widerspruch mehr! Danke, Digamma. Jetzt sollen sich erst noch andere zu deiner Auf-Klarung (sic!) äußern, dann will ich einen Einstellungsvorschlag machen - bzw. Digammas Erklärung müsste mit in den Namens-Gebungsteil einbezogen werden (und das bäte ich ihn selbst einzustellen, denn eine Feder eines anderen sollte man sich nicht an den Hut stecken).
- Und @ Digamma: wir sehen uns mit deiner Aussage wieder bei der Definition des Wurzel-Begriffs. Seit 1,5 Jahren liegt mir die Sache am Herzen. Damals hatte ich beim Wurzel- und Potenzbegriff so peinliche Fehler ausgessagt wie hier mit dem "Quotienten als dem Wert einer Subtraktion". Diese Fehler hatte ich dann mit dem Fehlerbekenntnis aus der Dikussion gelöscht, siehe hier: Diskussion: Wurzel, Widerspruch im Lemma. Und dann war bis jetzt keine Zeit, die Sache wieder anzugehen - von der Wurzel her bei den Grundrechenarten. Ich hatte damals deine Erklärung auch nicht verstanden - jetzt fiel deine Erklärung differenzierter aus: leicht für mich zu verstehen. Ich bin jetzt für die nächsten Stunden glücklich. Nochmals Danke.--Stefan B. Link (Diskussion) 21:30, 20. Dez. 2015 (CET)
Definition mangelhaft?[Quelltext bearbeiten]
Im Lemma liegt keine Definition vor. Zwar wird im Lemma gesagt, dass die Multiplikation eine der vier Grundrechenarten ist – aber damit wird noch nicht gesagt, was das Spezifikum der Multiplikation gegenüber den anderen Grundrechenarten ist. Auch wird im Lemma gesagt, dass die Multiplikation die Umkehroperation der Division ist – aber damit wird immer noch nichts Begriffsbestimmendes über die Multiplikation ausgesagt, sondern es wird eine Aussage getroffen, die den zu bestimmenden Sachverhalt des Multiplizierens voraussetzt. Es soll aber doch im Lemma gesagt werden, was denn dieser Sachverhalt des Multiplizierens ist. Ich mache einen analogen Vorschlag zu den Definitionen im Artikel Summe und Subtraktion:
- Unter Multiplikation versteht man das Vervielfältigen einer Zahl durch eine andere Zahl.
Sehr wohl wird im Punkt "Namensgebung" eine Definition gegeben:
- Die Multiplikation natürlicher Zahlen entsteht durch das wiederholte Addieren (Zusammenzählen) des gleichen Summanden.
Aber die Definition gehört laut Wikipedia-Richtlinien ins Lemma.
Benutzer Fritzbruno schrieb im vorherigen Diskussionspunkt, dass bei bei der Multiplikation komplexer Zahlen der Begriff Wert, bezogen auf die rechte Seite einer Multiplitation-Gleichung, kaum zu gebrauchen sei. Hier interessiert jetzt nicht die Richtigkeit dieses Satzes, sondern dass in der Definition von "natürlichen Zahlen" gesprochen wird. Wenn eine Multiplikation mit allen Zahlenarten verknüft werden kann, muss das denn nicht auch in die Definition der Multiplikation hinein? Oder soll sich dieser Artikel nur auf die Multiplikation der natürlichen Zahlen beziehen, statt auch z. B. auf die Multiplikation von komplexen Zahlen?--Stefan B. Link (Diskussion) 13:24, 21. Dez. 2015 (CET)
- Service Lemma (Lexikographie). --Rôtkæppchen₆₈ 22:45, 23. Dez. 2015 (CET)
- Liebes Rotkäppchen68, es gibt einen Unterschied zwischen dem Artikel "Lemma" und dem, wie das Lemma in Wikipedia aussehen soll. Vergleiche hierzu den Artikel Wie schreibe ich gute Artikel, dann den Punkt Begriffsdefinition und Einleitung. Du kannst nicht vom Artikel "Lemma" auf jenen Lemma-Begriff schließen, wie er in Wikipedia gelten soll.--Stefan B. Link (Diskussion) 07:28, 24. Dez. 2015 (CET)
- @Stefan B. Link, "Lemma" ist der Titel des Artikels, das im Artikel behandelte Stichwort. Was du meinst, ist nicht das Lemma, sondern die Einleitung. Gruß, --Digamma (Diskussion) 09:59, 24. Dez. 2015 (CET)
- Es ist leider nicht das erste Mal, dass Stefan hier seine eigenen Argumente durch falsche Wortwahl ruiniert. --Rôtkæppchen₆₈ 18:58, 24. Dez. 2015 (CET)
- Liebes Rôtkæppchen₆₈, es verdient jede Äußerung eines Diskutanten eine inhaltiche Auseinanderstetzung, denn jeder müht sich, eine Bewertung abzugeben. Ich will mich nur jetzt nicht einer argumentativen Entgegnung stellen, weil dies vom Thema abführte. Wenn du Wert darauf legst, dann in einem Punkt weiter unten. --Stefan B. Link (Diskussion) 08:50, 25. Dez. 2015 (CET)
- Es ist leider nicht das erste Mal, dass Stefan hier seine eigenen Argumente durch falsche Wortwahl ruiniert. --Rôtkæppchen₆₈ 18:58, 24. Dez. 2015 (CET)
- @ Digamma, lieber Digamma, BegriffsDefinition und Einleitung gehören laut Wikipedia-Richtlinien zusammen, Zitat: "Begriffsdefinition und Einleitung eröffnen den Artikel und leiten zum ersten Abschnitt über. Sie sollten das Lemma als Bezeichnung klären und dem Begriff nach in seiner Grundbedeutung erläutern."
- Momantan fehlt in der Artikel-Eröffnung (Lemma + Einführung vor einem ersten Abschnitt) das Lemma. Stimmt das?
- Ich will jetzt nicht den Punkt diskutieren, dass die momentane Einleitung - vergleicht man diese mit den entsprechenden Abschnitten im Thema Summe - verbesserungswürdig ist. Das will ich in in einem folgenden Diskussionsabschnitt erläutern, denn sonst wird die Diskussion unübersichtlich.--Stefan B. Link (Diskussion) 08:16, 25. Dez. 2015 (CET)
- @Stefan B. Link, "Lemma" ist der Titel des Artikels, das im Artikel behandelte Stichwort. Was du meinst, ist nicht das Lemma, sondern die Einleitung. Gruß, --Digamma (Diskussion) 09:59, 24. Dez. 2015 (CET)
- Liebes Rotkäppchen68, es gibt einen Unterschied zwischen dem Artikel "Lemma" und dem, wie das Lemma in Wikipedia aussehen soll. Vergleiche hierzu den Artikel Wie schreibe ich gute Artikel, dann den Punkt Begriffsdefinition und Einleitung. Du kannst nicht vom Artikel "Lemma" auf jenen Lemma-Begriff schließen, wie er in Wikipedia gelten soll.--Stefan B. Link (Diskussion) 07:28, 24. Dez. 2015 (CET)
Was genau fehlt in der Definition/Einleitung? Die beiden Definitionen/Einleitungen von Summe und Differenz sind mindestens genauso nichtssagend. Wenn es eine einfache Definition gäbe, müssten die Schulkinder diese Rechenoperationen nicht in einem langen Prozess lernen - und dies quasi jedes mal neu für jede Erweiterung des Zahlenraums. --Fritzbruno (Diskussion) 13:29, 26. Dez. 2015 (CET)
Summenformel richtig ?[Quelltext bearbeiten]
Ich weiss gar nicht was bei dieser Summelformel die Zählvariable i soll. Wenn der folgenden Satz richtig ist : 3 * 4 = 4 + 4 + 4, (so wie es auch im Artikel richtigerweise steht), dann müsste die Summenformel ganz andes aussehen:
Summe von i= 1 bis a : a = b1 + b2 + b3 + b4 ....ba.
So, wird eine Multiplikation in eine Summenreihe aufgelöst, wie ich finde. Mit dieser "Summenformel" kann ich rein gar nichts anfangen. War hier wieder ein "Mathematikprofessor" am Werk ?? :) 31.18.88.175 19:28, 15. Mär. 2016 (CET)
- so wie es im Artikel steht ist es richtig. Du machst den Fehler anzunehmen, dass jeder Summand unterschiedlich ist, also b1+b2+b3+ ...+ ba, in der Formel taucht aber gar kein Index auf, also steht da nur b+b+b+...+b, a mal dasselbe b. Reicht das? Erledigt --Fritzbruno (Diskussion) 20:04, 16. Mär. 2016 (CET)
- Wenn es um die folgende Formel
- gleich im ersten Abschnitt geht: Hier halte ich den Teil mit dem Summenzeichen auch für überflüssig. Es geht ja nicht um eine formale Definition (die müsste man rekursiv machen), sondern nur um eine Erklärung. Die kompliziertere Formulierung mit dem Summenzeichnen erklärt aber auch nicht mehr oder besser als die Summe mit den Pünktchten. Ich würde (und werde) diesen Term einfach streichen. Es geht damit nichts verloren. --Digamma (Diskussion) 21:12, 16. Mär. 2016 (CET)
- Done. --Digamma (Diskussion) 21:19, 16. Mär. 2016 (CET)
- Wenn es um die folgende Formel
Etymologie wünschenwert?[Quelltext bearbeiten]
wäre die Etymologie erwähnenswert?--212.25.31.181 16:15, 6. Jun. 2016 (CEST)
- Du meinst, über das hinaus, was schon im Artikel steht? --Digamma (Diskussion) 16:18, 6. Jun. 2016 (CEST)
Vedische Multiplikation[Quelltext bearbeiten]
Leider werden in meinem Browser (Firefox) die Beispiele zur Vedische Multiplikation komplett durcheinander wiedergegeben. Madyno (Diskussion) 14:03, 21. Okt. 2017 (CEST)
- Die Beispiele sind mit festen Umbrüchen formatiert. Damit das korrekt dargestellt wird, muss das Fenster eine gewisse Mindestbreite haben. --Rôtkæppchen₆₈ 20:24, 21. Okt. 2017 (CEST)
- Ich dachte, bei dieser Formatierung werden die Zeilen nicht umgebrochen. Anscheinend ist das doch der Fall. Habe ich mich getäuscht? Oder weißt du eine Möglichkeit, das besser zu machen? --Digamma (Diskussion) 20:34, 21. Okt. 2017 (CEST)
- Ich bin gerade dabei, an einer Tabelle zu basteln, aber es klappt leider noch nicht so, wie ich mir das vorstelle. So
- Ich dachte, bei dieser Formatierung werden die Zeilen nicht umgebrochen. Anscheinend ist das doch der Fall. Habe ich mich getäuscht? Oder weißt du eine Möglichkeit, das besser zu machen? --Digamma (Diskussion) 20:34, 21. Okt. 2017 (CEST)
|
|
|
|
- ist das schonmal ein Fortschritt. Es ist aber auch nicht quetschfest. --Rôtkæppchen₆₈ 21:01, 21. Okt. 2017 (CEST)
Simple German for Dummies[Quelltext bearbeiten]
Schade. Leider scheint es diesen Artikel (bisher) noch nicht in Leichter Sprache zu geben ... ;-( 46.114.140.152 11:46, 22. Okt. 2020 (CEST)
Warum leitet der hierher weiter, wenn dieser Satz hier gar nicht besprochen wird? (Oder hab ich schlecht gesucht?) Um die Frage selbst zu beantworte: wahrscheinlich weil der Redirect 2006 angelegt wurde und seither niemand drüber nach gedacht hat. Ich tendiere dazu, zu sagen, er hat einen eigenen Artikel verdient (wie auch in anderen Sprachen: Zero-product property, Équation produit-nul, …). Meinungen? --dingensfünf 16:44, 12. Nov. 2020 (CET)
- Nun ja, er scheint auch in enwiki oder frwiki nicht als »Satz« gehandelt zu werden. Ich hab das REDIRECT auf Nullteiler (eigentlich nullteilerfrei) geändert. Nullteilerfreiheit ist halt die Eigenschaft aller aus den natürlichen Zahlen entstehenden Zahlbereiche . Und das muss ja mit dem »Satz vom Nullprodukt« gemeint sein. –Nomen4Omen (Diskussion) 19:49, 12. Nov. 2020 (CET)
- Das finde ich jetzt blöd, ich hatte extra hier eine Diskussion angestoßen, statt einfach zu machen, jetzt machst du einfach. Und das auch noch denkbar ungeschickt: „Nullteiler“ ist quasi das Gegenteil von diesem Satz. Also ja, Nullteilerfreiheit ist eine Bedingung dass der Satz gilt – aber „Nullteiler“ ist das Gegenteil. Da der Satz vom Nullprodukt grundlegende Mittelstufenmathematik ist (aus eigener Erinnerung und wie man an den Google-Ergebnissen gut sieht), ist das jetzt maximal verwirrend (stell dir vor du lernst das grade und landest dann bei einem Artikel der sagt es gibt sowas, und natürlich überliest du das mit dem Ring weil das sagt dir nix). Ich hab das daher erstmal zurückgesetzt. Ich denke weiterhin, eigener Artikel ist gut. Dort kann man ja dann auf Nullteiler und so weiter verlinken. --dingensfünf 01:51, 13. Nov. 2020 (CET)
- @Dingens5: Das ist jetzt echt toll, dass du gemerkt hast, dass
- „Nullteiler“ quasi das Gegenteil von diesem «Satz vom Nullprodukt» ist.
- Also hast du das, was gemeint ist, sehr vermutlich kapiert!
- Einen eigenen Artikel ist das Thema m.E. nicht wert, obwohl es in enwiki oder frwiki ein eigener Artikel zu sein scheint. Immerhin wird es dort nicht als »Satz« gehandelt, sondern als »property« in enwiki und als »équation« in frwiki. (»property« ist gut, aber »équation« ist es eigentlich keine, sondern höchstens eine Implikation.)
- Die (wie du richtig erkannt hast) Nullteilerfreiheit ist eine Eigenschaft vieler –ohne Frage– wichtiger Ringe. Es gibt aber auch Ringe, die sie nicht haben. Insofern heißt der »Satz vom Nullprodukt« eigentlich:
- Der Ring der ganzen Zahlen ist nullteilerfrei.
- Oder:
- Alle Körper sind nullteilerfrei.
- M.a.W.: Sie enthalten keine (trivialen) Nullteiler.
- Ein «Satz vom Nullprodukt» wird nirgendwo im Artikel Multiplikation wirklich ausgesprochen oder auch nur angedeutet. Und ein «Satz vom Nullprodukt» kann überhaupt nicht mit der schlechthinnigen (wie hier suggeriert wird) Multiplikation identifiziert werden.
- NB1: Die Eigenschaft der Nullteilerfreiheit haben viele andere Ringe, z.B. der Ring der Gaußschen Zahlen und natürlich auch alle Körper, die selbstverständlich nebenbei auch Ringe sind.
- NB2: Die trivialen Nullteiler sind v.a. eine Folge des Distributivgesetzes (s. Ring (Algebra)#Folgerungen).
- Insofern ist die Sprechweise «Satz vom Nullprodukt» höchstens eine Kurzsprechweise, die IN KEINSTER WEISE als äquivalent zur Multiplikation angesehen werden kann. Denn –wie ich herauszuarbeiten versuche– gibt es Multiplikationen, die nullteilerfrei sind und solche, die es nicht sind. M.M.n. ist die Fragestellung VIEL besser bei nullteilerfrei aufgehoben als bei Multiplikation. Es kann sein, dass mehr als nur eine Weiterleitung zum Artikel wünschenswert ist. (Andererseits habe ich persönlich nie etwas von einem «Satz vom Nullprodukt» gehört. Seine frühen Versionen in dewiki sind ja auch so richtig bescheiden. M.a.W.: Ich könnte auf den Eintrag völlig verzichten und schlage die Löschung direkt vor. Die Aufruffrequenz in einem Jahr lag vor unserem Disput bei 1/Tag.) –Nomen4Omen (Diskussion) 19:21, 13. Nov. 2020 (CET)
- Die Bezeichnung "Satz vom Nullprodukt" ist im Schulunterricht üblich. Das Prinzip wird beim Lösungen von Gleichungen verwendet, daher kommt wohl das französische Lemma. --Digamma (Diskussion) 20:23, 13. Nov. 2020 (CET)
- @Dingens5: Das ist jetzt echt toll, dass du gemerkt hast, dass
- Danke! Dann hat der Eintrag wohl seine Berechtigung. Das ändert m.E. nichts daran, dass er eher zu Nullteiler als zu Multiplikation weiterleiten sollte. –Nomen4Omen (Diskussion) 20:39, 13. Nov. 2020 (CET)
- Hi nomen4omen. (ich versuche mal die Diskussion zu strukturieren, ich denke wir diskutieren hier mehrere Dinge parallel, daher die Nummerierung)
- I) Ich halte die Diskussion ob es jetzt ein Satz ist oder nicht, für nicht zielführend. Du hast recht, dass er nicht überall gilt. Aber: In den Strukturen, die typischerweise in der Schule behandelt werden, gilt er, deshalb denke ich, ist es völlig okay, dass er dort so genannt wird. Wir können ja erklären, dass er zwar "im Alltag" gilt, aber in den tatsächlich in den "Tiefen der Mathematik" nicht mehr überall. (Oder man könnte sagen: Der Satz wird üblicherweise verkürzt formuliert, vollständig lautet er "Wenn in einem nullteilerfreien Ring a·b=0, …")
- II) Zunächst ich wollte mit der Rück-Verschiebung keine entgültige Entscheidung vorwegnehmen, ich fand das neue Ziel nur so unpassend dass ich fand, lieber diskutieren wir in Ruhe und bis dahin lassen wir es wie es war, wenn das seit Jahren so ist kann es auch noch zwei Wochen so bleiben. Abgesehen davon finde ich aber wie gesagt die kommentarlose Weiterleitung zum Nullteiler derart verwirrend dass ich da wirklich sehr stark dagegen bin. Wir dürfen nicht vergessen, dass gerade dieses Lemma vorwiegend von mathematisch Unbedarften gesucht wird. Denen als erstes zu sagen "hey was du in der Schule gelernt hast, das gilt gar nicht", ist halt schädlich.
- III) Aus alledem leite ich ab: Ein eigener Artikel ist die einzige Möglichkeit, alle Bedürfnisse zu befriedigen. Der Artikel könnte erstmal die Basics erklären und wie man ihn anwendet; könnte aber dann noch mehr ins Detail gehen und erläutern, dass er tatsächlich nicht überall gilt, sondern dass Nullteilerfreiheit gegeben sein muss etc. Dann wäre er a) mathematisch korrekt, aber auch b) für Laien nicht verwirrend.
- IV) Und schließlich zur Aufruffrequenz: Kann es sein dass da nur Aufrufe des Artikels selbst gezählt werden? Wenn du mal den Satz googelst siehst du dass da eigentlich sehr viel "Beratungsbedarf" ist. Unter 1/Jahr kann ich mir nicht vorstellen. --dingensfünf 17:27, 15. Nov. 2020 (CET)
- @Dingens5: Also dann mach du mal ruhig deinen Artikel. –Nomen4Omen (Diskussion) 18:24, 15. Nov. 2020 (CET)
- @Dingens5: Nachdem von dir längere Zeit nichts gekommen ist, habe ich den Artikel Nullteiler leicht aufgebohrt und Satz vom Nullprodukt zum dortigen Abschnitt »Satz vom Nullprodukt« weitergeleitet. Ferner habe ich einen neuen Eintrag Nullprodukt angelegt, der auf den ganzen Artikel verlinkt.
- Das alles beißt sich nicht mit: einem von dir gefertigten Artikel. (Ich meinerseits würde einen solchen aber nicht benötigen.) –Nomen4Omen (Diskussion) 18:23, 23. Nov. 2020 (CET)
Inhalt des Lemmas[Quelltext bearbeiten]
Ich habe Zweifel, daß es sinnvoll ist, das Lemma nur auf eine Species, also eine rein algorithmische Angelegenheit, zu beziehen. Vielmehr sollte deutlich werden, daß die M. eine der beiden grundlegenden Operationen auf Körpern ist, und folglich auf ihre mathematische Bedeutung eingegangen werden. --95.112.90.145 07:42, 21. Feb. 2021 (CET)
- Sollte das nicht eher beim Artikel Körper (Algebra) geschehen? Die Multiplikation in Körpern hat ja keine eigenständige Bedeutung, losgelöst von den Körperaxiomen. --Digamma (Diskussion) 12:14, 21. Feb. 2021 (CET)
- Wieso "eher"? Es gibt im ganzen Artikel überhaupt keine Referenz auf Körper (Algebra), entsprechend wird der Begriff "M." auch in keiner Weise abstrakt betrachtet. Daß es z. B. auch so etwas wie Matrizenmultiplikation gibt, erfährt der Leser schlicht nicht, der wird gleich in der Einleitung damit abgespeist, die M. wäre eine der vier Species. Das ist doch nun deutlich zu sehr vereinfacht. --95.112.90.145 17:00, 21. Feb. 2021 (CET)
- Korrektur: Ähm, doch, Körper und die Körperaxiome stehen drin. Trotzdem: der Begriff ist zu sehr auf die Bedeutung "Grundrechenart" eingeengt. --95.112.90.145 17:22, 21. Feb. 2021 (CET)
- Es gibt ja den Abschnitt "Verallgemeinerungen", wo diese Dinge angesprochen und verlinkt werden. Was würdest du denn darüber hinaus noch aufnehmen? --Digamma (Diskussion) 20:38, 21. Feb. 2021 (CET)
- Es geht nicht um ein "darüber hinaus", denn das würde implizieren, daß "der Rest" schon so in Ordnung ist. Ist er aber nicht, sondern es gibt ein grundlegendes Strukturproblem: Die M. ist als Rechenoperation, also als algorithmischer Gegenstand, definiert. Richtig wäre ein dreiteiliger Aufbau: 1. Axiomatik: Die Multiplikation als grundlegende Operation in der Definition von Körpern und in der Linearen Algebra. 2. Algebraische Behandlung: Umformung von Termen unter Verwendung der algebraischen Regeln für die Multiplikation. 3. Arithmetik: das ist der Punkt, der im Artikel zum Lemma bisher fälschlicherweise fast ausschließlich behandelt wird. Dabei geht es aber tatsächlich "nur" um die Rechenoperation, also darum, wie in einem ziemlich beschränktem Umfang die Ergebnisse, die sich beim Einsetzen konkreter Zahlen in die Variablen multiplikativer Terme arithmetisch ermitteln lassen, und das zudem auch nur auf "Schulunterrichtsniveau" - der ganze relevante Bereich Computerarithmetik wird völlig ausgespart. - Meines Erachtens müßte der Artikel praktisch komplett neugestaltet werden, um das anzustrebende enzyklopädische Niveau zu erreichen. Vergleichsweise: der Artikel kommt mir derzeit vor, als ob im Artikel "Geometrie" die zweckmäßige Gestaltung von Knotenschnüren zur Vermessung von Grundstücken diskutiert würde. Ja, natürlich ist die mathematische Disziplin "Geometrie" historisch aus der Befassung mit Fragen zur Landvermessung entstanden, aber man kann sie doch nun wirklich nicht darauf einengen. Ebenso ist M. natürlich nicht eine Sammlung von Vorgehensweisen zur Ermittlung von alltäglichen Rechenergebnissen mit Papier und Bleistift. --77.0.188.221 06:43, 22. Feb. 2021 (CET)
- Es gibt ja den Abschnitt "Verallgemeinerungen", wo diese Dinge angesprochen und verlinkt werden. Was würdest du denn darüber hinaus noch aufnehmen? --Digamma (Diskussion) 20:38, 21. Feb. 2021 (CET)
- Korrektur: Ähm, doch, Körper und die Körperaxiome stehen drin. Trotzdem: der Begriff ist zu sehr auf die Bedeutung "Grundrechenart" eingeengt. --95.112.90.145 17:22, 21. Feb. 2021 (CET)
- Wieso "eher"? Es gibt im ganzen Artikel überhaupt keine Referenz auf Körper (Algebra), entsprechend wird der Begriff "M." auch in keiner Weise abstrakt betrachtet. Daß es z. B. auch so etwas wie Matrizenmultiplikation gibt, erfährt der Leser schlicht nicht, der wird gleich in der Einleitung damit abgespeist, die M. wäre eine der vier Species. Das ist doch nun deutlich zu sehr vereinfacht. --95.112.90.145 17:00, 21. Feb. 2021 (CET)
Multiplikation als Kopfrechnung[Quelltext bearbeiten]
Ich hatte vor geraumer Zeit den Abschnitt gelöscht. Inhaltlich stellt er einen ziemlichen Spezialfall vor, der so in der Praxis so gut wie nie auftritt. Dafür einen eigenen Abschnitt einzufügen mit irreführender Bezeichnung ist m.E. unsinnig. Die Grundlagen für Multiplikation im Kopf werden im 1x1 gelegt, falls dieser Spezialfall eine Bedeutung haben sollte (wofür jeglicher Beleg fehlt) wäre er bestenfalls dort unterzubringen. Wenn jetzt hier also nicht unerwartete schlüssige Argumente für die Beibehaltung erscheinen werde ich den Abschnitt wieder entsorgen. --Fritzbruno (Diskussion) 11:27, 12. Dez. 2021 (CET)
- Gelöscht!Erledigt--Petrus3743 (Diskussion) 18:53, 12. Dez. 2021 (CET)
- Servus Fritzbruno,
- leider kann ich deine Argumentation aus folgenden Gründen nicht nachvollziehen:
- Diese Möglichkeit der Kopfrechnung, du nennst sie Spezialfall (bis 99 x 91 sind es 45 mögliche Anwendungen), wird im Artikel Kopfrechnen mit Beleg auf eine andere Art beschrieben, die vielleicht für Grundschülerinnen und Grundschüler nicht sofort verständlich ist.
- Es fehlt die Begründung für ... mit irreführender Bezeichnung.
- Mich überrascht deine Aufgeregtheit. Du, ein geschätzter und altdienender Mitstreiter, weiß doch, in der WP wird gerne ein freundlicher Umgang und die Wertschätzung der Arbeit eines anderen gesehen.
- Da ich, zu der mir aus der Schulzeit bekannten Methode, keinen zusätzlichen und einsehbaren Beleg aus der Sekundärliteratur finden konnte, sondern nur ein Beispiel, habe ich den betreffenden Abschnitt gelöscht. Eine dritte Meinung hierzu wäre m. E. hilfreich. Mit Gruß--Petrus3743 (Diskussion) 10:24, 13. Dez. 2021 (CET)
- ganz kurz dazu: 1. Danke für's Löschen 2. Aufgeregtheit? Beachte bitte die Zeitabstände meiner Bearbeitungen! 3. Dass der gelöschte Teil nur einen Spezialfall darstellte belegt der entsprechende Abschnitt beim Kopfrechnen, dort steht er nicht umsonst zwischen ein paar anderen ähnlichen Spezialfällen. Unter "Multiplikation als Kopfrechnung" würde ich nicht nur einen Spezialfall (für 45 mögliche Anwendungen) von mehreren erwarten sondern allgemeine Regeln. --Fritzbruno (Diskussion) 18:21, 1. Feb. 2022 (CET)
Quelle für die David Harvey – Joris van der Hoeven – Arbeit[Quelltext bearbeiten]
In der angegebenen Quelle konnte ich den Volltext nicht finden. Hier fand ich ihn: https://hal.archives-ouvertes.fr/hal-02070778/file/nlogn.pdf . --Himbeerbläuling (Diskussion) 07:39, 22. Feb. 2022 (CET)
- Servus Himbeerbläuling, ein besonderes Dankeschön für den Link. Erledigt Mit Gruß--Petrus3743 (Diskussion) 11:46, 22. Feb. 2022 (CET)













![{\displaystyle {\begin{matrix}\underbrace {b+b+\cdots +b} \\{a}\\[-4ex]\end{matrix}}=\sum _{i=1}^{a}b=a\cdot b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e4d038172921f4124ce9ee09d98bd180da68c9)

