Fermatsche Spirale


Eine fermatsche oder parabolische Spirale ist eine nach Pierre de Fermat benannte ebene Kurve, die sich in Polarkoordinaten durch die Gleichung
einer Parabel (mit horizontaler Achse) beschreiben lässt.
Die fermatsche Spirale sieht der archimedischen Spirale ähnlich. Im Gegensatz zu ihr hat sie aber abnehmenden Windungsabstand, d. h., die Windungen liegen nach außen hin immer dichter.
So wie andere Spiralen werden auch fermatsche Spiralen zur Konstruktion von krümmungsstetigen Übergangskurven verwendet.[1]
Beschreibung in kartesischen Koordinaten[Bearbeiten | Quelltext bearbeiten]
Die fermatsche Spirale mit der Polargleichung
lässt sich in kartesischen Koordinaten durch die Parameterdarstellung
beschreiben.
Aus der Parameterdarstellung und ergibt sich eine Darstellung mit einer Gleichung:
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Zerlegung der Ebene[Bearbeiten | Quelltext bearbeiten]

Eine vollständige fermatsche Spirale (beide Äste) ist, im Gegensatz zu einer archimedischen oder hyperbolischen Spirale, eine glatte doppelpunktfreie Kurve, die die Ebene, wie eine Gerade oder ein Kreis oder eine Parabel, in zwei zusammenhängende Bereiche zerlegt. Die besondere Herausforderung bei der Zerlegung der Ebene durch eine fermatsche Spirale ist, dass man mit bloßem Auge nicht so leicht wie bei Gerade, Kreis oder Parabel entscheiden kann, auf welcher Seite der Kurve ein Punkt liegt.
Krümmung[Bearbeiten | Quelltext bearbeiten]
Mit der Formel
für die Krümmung einer Kurve in Polardarstellung und den Ableitungen und der fermatschen Spirale ergibt sich für die Krümmung
Im Nullpunkt ist die Krümmung . Die vollständige Spirale hat also
- im Nullpunkt einen Wendepunkt mit der x-Achse als Wendetangente.

Inversion[Bearbeiten | Quelltext bearbeiten]
Die Spiegelung am Einheitskreis (Inversion) lässt sich in Polarkoordinaten durch beschreiben.
- Das Bild der fermatschen Spirale bei der Spiegelung am Einheitskreis ist eine Lituus-Spirale mit .
Für schneiden sich beide Kurven in einem Fixpunkt auf dem Einheitskreis.
- Die Wendetangente (-Achse) der fermatschen Spirale (im Nullpunkt) geht bei der Spiegelung in sich über und ist die Asymptote der Lituus-Spirale.
Fläche zwischen Kurvenbögen[Bearbeiten | Quelltext bearbeiten]
Die Sektorfläche für den Kurvenbogen zwischen und ist
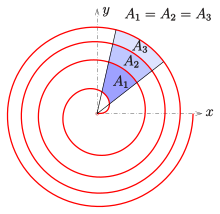
Flächen zwischen Kurvenbögen
Erhöht man beide Winkel um , ergibt sich
Der Inhalt der Sektorfläche zwischen den Kurven ist also
hängt nur von der Differenz der beiden Winkel und nicht von den Winkeln selbst ab.
In dem Beispiel (siehe Bild) haben also alle benachbarten Sektorstreifen denselben Inhalt: .
Diese Eigenschaft der fermatschen Spirale spielt in der Elektrotechnik bei der Herstellung von Drehkondensatoren eine Rolle.[2]

- Spezialfall von Fermat
1636 berichtete Fermat in einem Brief[3] an Marin Mersenne den folgenden Spezialfall:
Es seien . Dann ist der Inhalt der schwarzen Fläche (siehe Bild) die Hälfte der Fläche des Kreises mit Radius . Die Zwischenflächen (weiß, blau, gelb) haben den Inhalt Also gilt:
- Der Flächeninhalt zwischen zwei Spiralbögen nach einer ganzen Umrundung ist gleich dem Flächeninhalt des Kreises .
Bogenlänge[Bearbeiten | Quelltext bearbeiten]
Die Länge des Bogens einer fermatschen Spirale zwischen zwei Punkten lässt sich mit der Formel für Kurven in Polardarstellung berechnen:
Die Lösung dieses Integrals ist allerdings nur numerisch oder mit Hilfe eines elliptischen Integrals möglich.
Die Bogenlänge des positiven Zweiges der fermatschen Spirale vom Ursprung aus kann auch durch die gaußsche hypergeometrische Funktion und der unvollständigen eulerschen Betafunktion dargestellt werden:[4]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Anastasios M. Lekkas1, Andreas R. Dahl, Morten Breivik, Thor I. Fossen4: Continuous-Curvature Path GenerationUsing Fermat’s Spiral. In: Modeling, Identification and Control. Vol. 34, No. 4, 2013, S. 183–198, ISSN 1890-1328.
- ↑ Fritz Wicke: Einführung in die höhere Mathematik. Springer-Verlag, 2013, ISBN 978-3-662-36804-6, S. 414.
- ↑ Lettre de Fermat à Mersenne du 3 juin 1636, dans Paul Tannery. In: Oeuvres de Fermat. T. III, S. 277, Lire en ligne.
- ↑ Eric W. Weisstein: Fermat's Spiral. Abgerufen am 4. Februar 2023 (englisch).
Literatur[Bearbeiten | Quelltext bearbeiten]
- Friedrich Grelle: Analytische Geometrie der Ebene, Verlag F. Brecke, 1861 [1], S. 213.
- Jac. Phil Kulik: Spirallinien in Lehrbuch der höhern Analysis, Band 2, In Commiss. bei Kronberger u. Rziwnatz, 1844, [2], S. 226.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Fermat’s Spiral. In: MathWorld (englisch).
- Mathcurve: Fermatsche Spirale



































