Methode von Swale

Nach der Methode von Swale lässt sich der Radius eines gegebenen Kreises , dessen Mittelpunkt und dessen Radius nicht eingezeichnet sind, mit Hilfe von nur zwei Kreisbögen und zwei Strecken konstruieren.
Ross Honsberger stellt die Methode als Problem Nr. 48 in seinem Buch Mathematical Morsels (deutsch: Gitter-Reste-Würfel) dar, ohne näher auf Swale einzugehen.[1] Er verweist dazu auf die Lösung eines Problems in der Zeitschrift Pi Mu Epsilon aus dem Jahr 1951.
Problemstellung[Bearbeiten | Quelltext bearbeiten]
Der Radius eines gegebenen Kreises , dessen Mittelpunkt und dessen Radius nicht eingezeichnet sind, ist mit Hilfe von zwei Kreisbögen und zwei Strecken zu konstruieren. Die Konstruktion ist zu begründen.
Konstruktionsbeschreibung[Bearbeiten | Quelltext bearbeiten]
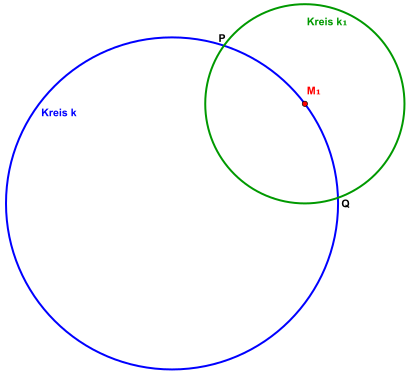
1. Konstruktionsschritt:
- Markiere einen Punkt auf der Kreislinie von und zeichne einen Kreis um , dessen Radius beliebig so gewählt ist, dass er den Kreis in den Punkten und schneidet.
2. Konstruktionsschritt:
- Zeichne einen Kreis um mit dem Radius , der den Kreis im Punkt des Kreisinneren von schneidet.
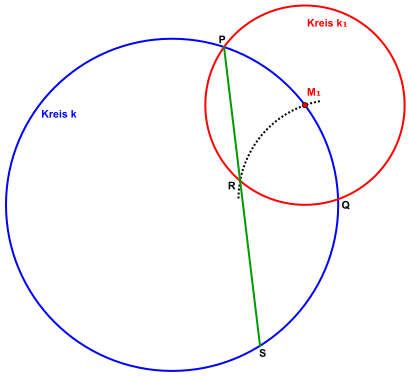
3. Konstruktionsschritt:
- Zeichne eine Strecke von zu einem Punkt von , auf der der Punkt liegt.
4. Konstruktionsschritt:
- Zeichne die Strecke . Deren Länge ist der Radius von .
Grafische Darstellung der Konstruktionsschritte (Die hinzugekommenen Schritte sind jeweils grün markiert.):
-
Schritt 1
-
Schritt 2
-
Schritt 3
-
Schritt 4
Begründung der Konstruktion[Bearbeiten | Quelltext bearbeiten]
(Die Begründungsschritte basieren auf der obigen Planfigur.)
- Jede Seite des Dreiecks ist so lang wie der Radius von . Deshalb ist das Dreieck gleichseitig mit dem Innenwinkel der Weite 60°.
- Der zu gehörige Peripheriewinkel hat die Weite 30°, da er halb so groß ist wie der zugehörige Mittelpunktswinkel mit der Weite 60°.
- ist zugleich auch der zu gehörige Peripheriewinkel. Deshalb hat der Mittelpunktswinkel des Kreises die Weite 60° und ist damit Innenwinkel des Dreiecks , welches folglich gleichseitig ist.
- Der Radius des Kreises ist somit die Seitenlänge des gleichseitigen Dreiecks .
Vergleich mit der Konstruktion des Radius anhand zweier Mittelsenkrechten[Bearbeiten | Quelltext bearbeiten]

Normalerweise werden die Mittelsenkrechten zweier benachbarter Sehnen konstruiert, um zunächst den Kreismittelpunkt als Schnittpunkt der beiden Mittelsenkrechten zu erhalten. Daraus ergibt sich der Radius durch Verbinden des Mittelpunkts mit einem Punkt der Kreislinie. Man benötigt hierzu mindestens drei Kreisbögen und zwei Strecken, nämlich die beiden Sehnen, während die Methode von Swale nur zwei Kreisbögen, nämlich und den Kreis um mit Radius , sowie zwei Strecken, nämlich und , benutzt.[1][2]
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b Ross Honsberger: Gitter - Reste - Würfel Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig 1984, ISBN 978-3-528-08476-9, S. 121 und 122
- ↑ Leo Moser: PROBLEM DEPARTMENT. Pi Mu Epsilon Journal, vol. 1, no. 4, 1951, p. 146 (Lösung von Ding Hwang, University of California)










![{\displaystyle [SQ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88349f0cfe65e955af39f4163ccda01fe6f782f8)