Quantilsregression
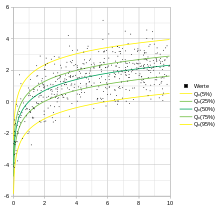
Als Quantilsregression wird eine Methode zum Schätzen der Parameter eines linearen Regressionsmodells bezeichnet. Im Gegensatz zur Kleinste-Quadrate-Schätzung, die den Erwartungswert der Zielgröße schätzt, ist die Quantilsregression dazu geeignet, ihre bedingten Quantile zu schätzen. Die Quantilsregression ist somit eine Möglichkeit durch die Betrachtung anderer Eigenschaften der Zielgrößenverteilung, den dem klassischen linearen Modell unterliegenden Fokus auf den Erwartungswert der Zielgröße aufzugeben.[1] Die Median-Regression stellt einen Spezialfall der Quantilsregression dar.
Optimierungsproblem[Bearbeiten | Quelltext bearbeiten]

Sei eine reelle Zufallsvariable mit Verteilungsfunktion , dann entspricht das (bedingte) -Quantil von :
mit
Seien mit beobachtete Paare von unabhängigen Variablen und zugehörigen abhängigen Variablen . Das Regressionsmodell wird als beschrieben, wobei prinzipiell auch nichtlineare Zusammenhänge angenommen werden können. Die optimalen Regressionsparameter können durch die folgende empirische Risikominimierung bestimmt werden:[2][3]
- .
Hierbei entspricht dem linearen Prädiktor. Die Verlustfunktion entspricht der geneigten absoluten Abweichung:
Aufgrund ihres Aussehens wird die Verlustfunktion auch pinball loss genannt.[4]
Das Optimierungsproblem kann mit typischen Optimierungsalgorithmen gelöst werden.
Beachte, dass die Unsicherheit extremer Quantile tendenziell größer ist, da die Wahrscheinlichkeitsdichte der zugrundeliegenden Verteilung dort sehr kleine Werte annimmt, siehe Empirisches Quantil#Eigenschaften:
wobei das Quantil ist, die Stichprobengröße und der Wert der Zufallsvariable beim p-Quantil.
Erweiterungen[Bearbeiten | Quelltext bearbeiten]
Zensierte Daten[Bearbeiten | Quelltext bearbeiten]
Für unzensierte Daten kann die normale Quantilsregression (mit Zielvariable Ereigniszeit) ebenso wie die nichtparametrische Ereigniszeitanalyse benutzt werden um die bedingten empirischen Quantile zu schätzen: bei der Ereigniszeitanalyse wird die (bedingte) Überlebensfunktion geschätzt und aus dieser kann der bedingte Quantilsschätzer direkt abgelesen werden.

Für zensierte Daten muss die Quantilsregression zur zensierten Quantilsregression erweitert werden[5] und liefert dann eine Verallgemeinerung des Kaplan-Meier-Schätzers[6].
Schätzung mehrerer Quantile[Bearbeiten | Quelltext bearbeiten]
Die simultane Schätzung mehrerer Quantile mithilfe der empirischen Likelihood kann zu effizienteren Schätzer führen als wenn nur ein Quantil geschätzt wird[7].
Literatur[Bearbeiten | Quelltext bearbeiten]
- Ludwig Fahrmeir, Thomas Kneib, Stefan Lang, Brian D. Marx: Regression – Models, Methods and Applications. Springer, Berlin / Heidelberg 2013, ISBN 978-3-642-34332-2, Kapitel 10: Quantile Regression, doi:10.1007/978-3-642-34333-9 (E-Book-ISBN 978-3-642-34333-9).
- David J. Petersen et al.: Perspektiven einer pluralen Ökonomik. Springer Vieweg. Springer Fachmedien, Wiesbaden 2019, ISBN 978-3-658-16144-6, S. 238–240.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ David J. Petersen et al.: Perspektiven einer pluralen Ökonomik. Springer Vieweg. Springer Fachmedien, Wiesbaden 2019, ISBN 978-3-658-16144-6, S. 238.
- ↑ Roger Koenker, Gilbert Basset Jr.: Regression Quantiles. In: Econometrica: journal of the Econometric Society. 1978, S. 33–50.
- ↑ Roger Koenker, Kevin F. Hallock: Quantile regression. In: Journal of economic perspectives. Band 15, Nr. 4, 2001, S. 143–156.
- ↑ Ingo Steinwart, Andreas Christmann: Estimating conditional quantiles with the help of the pinball loss. In: Bernoulli. Band 17, Nr. 1, Februar 2011, ISSN 1350-7265, S. 211–225, doi:10.3150/10-BEJ267, arxiv:1102.2101 (projecteuclid.org [abgerufen am 11. Juli 2020]).
- ↑ Portnoy, Stephen. "Censored quantile regression." Journal of American Statistical Association 98.1 (2003): 00.
- ↑ Handbook of Quantile Regression. (2017). Vereinigtes Königreich: CRC Press. Seiten 80 ff. Google Books
- ↑ Cho, Hyunkeun & Kim, Seonjin & Kim, Mi-Ok, 2017. "Multiple quantile regression analysis of longitudinal data: Heteroscedasticity and efficient estimation," Journal of Multivariate Analysis, Elsevier, vol. 155(C), pages 334-343.




























