Benutzer:Saure/Werkstatt
Prinzip der Differentialrechnung[Bearbeiten | Quelltext bearbeiten]

Das Beispiel des letzten Abschnitts ist besonders einfach, wenn die Zunahme der Strecke des Autos mit der Zeit gleichförmig, also linear verläuft. Man spricht in diesem Falle auch von einer Proportionalität zwischen Zeitspanne und Strecke, wenn zu Beginn der Aufzeichnung () noch keine Strecke zurückgelegt wurde (). Dies hat eine immer gleichbleibende Veränderung der Strecke in einem bestimmten Zeitintervall zur Folge, egal ab wann die Messung startet. Beispielsweise legt das Auto zwischen 0 und 1 Sekunden eine gleich lange Strecke zurück wie zwischen 9 und 10 Sekunden. Nimmt man an, dass sich das Auto für jede verstrichene Sekunde 2 Meter weiter bewegt, so hat die Proportionalität zur Folge, dass es sich für jede halbe Sekunde nur um 1 Meter zurück legt usw. Als Proportionalitätsfaktor gilt also über den ganzen Weg die konstante Geschwindigkeit , wobei im Beispiel beträgt.
Allgemein bewegt sich das Auto in der Zeitspanne um insgesamt die Strecke vorwärts. Bei ergibt sich ein Wegstück .
Falls der Startwert nicht sondern beträgt, ändert dies nichts, da sich die Konstante in der oberen Differenz stets heraussubtrahiert. Auch anschaulich ist dies vernünftig: Die Startposition des Autos sollte bei gleichförmiger Bewegung unerheblich für dessen Geschwindigkeit sein.
Es lässt sich also festhalten:
- Lineare Funktionen. Für lineare Funktionen (man beachte, dass es keine Ursprungsgerade sein muss) ist der Ableitungsbegriff wie folgt erklärt. Hat die betrachtete Funktion die Gestalt , so hat die momentane Veränderungsrate in jedem Punkt den Wert , es gilt also für die zugehörige Ableitungsfunktion . Die Ableitung lässt sich aus den Daten also direkt ablesen. Insbesondere gilt: Jede konstante Funktion hat die Ableitung , da sich mit Abänderung der Eingabewerte nichts am Ausgabewert ändert. Das Maß der Veränderung beträgt also überall 0.
Mitunter deutlich schwieriger kann es werden, wenn eine Bewegung nicht gleichförmig verläuft. In diesem Falle sieht der Verlauf der Zeit-Strecken-Funktion ggf. ganz anders aus als eine Gerade. Aus der Beschaffenheit der Zeit-Strecken-Funktion lässt sich dann ablesen, dass die Bewegungsverläufe des Autos sehr vielseitig sind, was zum Beispiel mit Verkehrsampeln, Kurven, Staus und anderen Verkehrsteilnehmern zu tun haben kann. Da solche Arten von Verläufen besonders häufig in der Praxis anzutreffen sind, ist es zweckmäßig, den Ableitungsbegriff auch auf nicht-lineare Funktionen auszudehnen. Hier stößt man jedoch schnell auf das Problem, dass es auf den ersten Blick keinen klaren Proportionalitätsfaktor gibt, der genau die lokale Veränderungsrate ausdrückt. Die einzig mögliche Strategie sieht daher vor, eine Linearisierung der nicht-linearen Funktion vorzunehmen, um das Problem auf den einfachen Fall einer linearen Funktion zurückzuführen. Diese Technik der Linearisierung bildet den eigentlichen Kalkül der Differentialrechnung und ist in der Analysis von sehr großer Bedeutung, da sie dabei hilft, komplizierte Prozesse lokal auf sehr leicht verständliche Prozesse, nämlich lineare Vorgänge, zu reduzieren.[1]
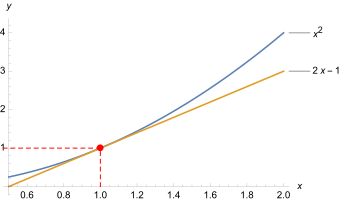
Die Strategie kann exemplarisch an der nicht-linearen Funktion erläutert werden.[2] Die folgende Tabelle zeigt die Linearisierung der quadratischen Funktion an der Stelle 1.
| 0,5 | 0,75 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,1 | 2 | 3 | 4 | 100 | |
| 0,25 | 0,5625 | 0,9801 | 0,998001 | 1 | 1,002001 | 1,0201 | 1,21 | 4 | 9 | 16 | 10000 | |
| 0 | 0,5 | 0,98 | 0,998 | 1 | 1,002 | 1,02 | 1,2 | 3 | 5 | 7 | 199 |
Dass die Linearisierung nur ein lokales Phänomen ist, zeigt die größer werdende Abweichung der Funktionswerte bei entfernteren Eingabewerten. Die lineare Funktion ahmt das Verhalten von nahe der Eingabe 1 sehr gut nach (besser als jede andere lineare Funktion). Im Gegensatz zu hat man es bei jedoch einfach, die Veränderungsrate an der Stelle 1 zu interpretieren: Sie beträgt (wie überall) genau 2. Damit gilt .
Es lässt sich also festhalten:
- Nicht-lineare Funktionen. Soll die momentane Veränderungsrate einer nicht-linearen Funktion in einem bestimmten Punkt ermittelt werden, so muss diese (wenn möglich) dort linearisiert werden. Anschließend ist die Steigung der approximativen linearen Funktion die lokale Veränderungsrate der betrachteten nicht-linearen Funktion, und es gilt die gleiche Anschauung wie bei Ableitungen linearer Funktionen. Insbesondere gilt, dass die Veränderungsraten einer nicht-linearen Funktion nicht konstant sind, sondern sich von Punkt zu Punkt ändern werden.
Die genaue Bestimmung der richtigen Linearisierung einer nicht-linearen Funktion an einer bestimmten Stelle ist zentrale Aufgabe des Kalküls der Differentialrechnung. Es geht um die Frage, ob sich aus einer Kurve wie berechnen lässt, welche lineare Funktion sie an einem gegebenen Punkt am besten annähert. Im Idealfall ist diese Berechnung sogar so allgemein, dass sie auf alle Punkte des Definitionsbereichs angewendet werden kann. Im Falle von kann gezeigt werden, dass an der Stelle die beste lineare Annäherung die Steigung besitzen muss. Mit der Zusatzinformation, dass die lineare Funktion die Kurve im Punkt schneiden muss, kann dann die vollständige Funktionsgleichung der approximierenden linearen Funktion ermittelt werden. In vielen Fällen reicht jedoch die Angabe der Steigung, also die Ableitung, aus.
Als Ansatzpunkt gilt die explizite Bestimmung des Grenzwerts des Differentialquotienten
woraus für sehr kleine h durch einfache Umformung der Ausdruck
hervorgeht. Die rechte Seite ist eine in lineare Funktion mit Steigung und ahmt in der Nähe von sehr gut nach. Bei einigen elementaren Funktionen wie Polynomfunktionen, trigonometrischen Funktionen, Exponentialfunktionen oder Logarithmusfunktionen kann durch diesen Grenzwertprozess eine Ableitungsfunktion bestimmt werden. Mit Hilfe sog. Ableitungsregeln kann dieser Prozess dann auf viele weitere Funktionen verallgemeinert werden, wie Summen, Produkte oder Verkettungen elementarer Funktionen wie der oben genannten.
Exemplarisch: Ist und , so wird das Produkt durch das Produkt der linearen Funktionen angenähert: , und durch Ausmultiplizieren:
womit die Steigung von bei genau entspricht.[3] Ferner helfen die Ableitungsregeln dabei, die mitunter aufwändigen Grenzwertbestimmungen durch einen „direkten Rechenkalkül“ zu ersetzen und damit den Ableitungsprozess zu vereinfachen. Aus diesem Grund werden Differentialquotienten in der Lehre zum fundamentalen Verständnis studiert und zum Beweisen der Ableitungsregeln verwendet, jedoch in der Rechenpraxis nicht angewendet.
Darstellung[Bearbeiten | Quelltext bearbeiten]
Bei Wechselgrößen muss beachtet werden, dass sich die Augenblickswerte der Spannung und der Stromstärke periodisch ändern. Am ohmschen Widerstand besteht die Proportionalität zwischen Spannung und Stromstärke nicht nur für Gleichgrößen, sondern auch für Augenblickswerte zum jeweils betrachteten Zeitpunkt. Weitere auch als lineare Widerstände bezeichnete elektrische Bauelemente reagieren zeitabhängig. Bei einem idealen elektrischen Kondensator ist die Stromstärke aufgrund der Kapazität proportional zur zeitlichen Änderung der Spannung. Die dem Kondensator von einem Erzeuger gelieferte Energie wird zum Aufbau eines elektrischen Feldes verwendet. Die Energie wird darin zunächst gespeichert. Später, nach dem Wechsel des Vorzeichens der Stromstärke, wird das Feld wieder abgebaut und die Energie zurückgespeist. – Entsprechend ist bei einer idealen Spule die Spannung aufgrund der Induktivität proportional zur zeitlichen Änderung der Stromstärke.
In den Rechnungen mit Wechselgrößen ergibt sich, dass bei diesen Bauelementen eine sinusförmige Stromstärke
mit der Frequenz oder der Kreisfrequenz eine zeitlich verzögerte, ebenfalls sinusförmige Spannung
mit derselben Kreisfrequenz zur Folge hat – oder umgekehrt. Das Beibehalten der Sinusform im zeitlichen Verlauf ist mit ein Grund, das Verhalten der genannten Bauelemente als linear zu bezeichnen. Allerdings stellt sich durch die Verzögerung ein Phasenverschiebungswinkel ein:
Er ist nur beim ohmschen Widerstand gleich null. Außer bei diesem ist das Verhältnis zeitabhängig, ohne Proportionalität und zur Beschreibung in der Wechselstromtechnik ungeeignet.[4] Sinnvoll angeben lässt sich jedoch der Quotient der zeitunabhängigen Amplituden (oder gleichwertig der Quotient der Effektivwerte), der als Scheinwiderstand
bezeichnet wird. Beim idealen Kondensator und bei der idealen Spule ist der Scheinwiderstand so groß wie der Betrag des Blindwiderstands . Beide Widerstände werden wie der ohmsche Widerstand als unabhängig von Spannung, Stromstärke und Zeit angesehen. Aber sie sind abhängig von einem Parameter, der Frequenz.
Bei einer realen Spule ist meistens der ohmsche Drahtwiderstand nicht gegenüber dem Blindwiderstand zu vernachlässigen. Da er Energie nach außen abgeben kann, wird er als Wirkwiderstand bezeichnet. Der Gesamtwiderstand ergibt sich allerdings wegen der unterschiedlichen Phasenverschiebungen nicht wie gewohnt durch arithmetische Addition. Der Phasenverschiebungswinkel beträgt bei der Induktivität +90°, bei der Kapazität −90°. Damit ist eine Pythagoreische Addition erforderlich:

Rechts: Deren Projektionen auf die senkrechte Ursprungsgerade ergeben die Augenblickswerte, sie haben über dem Phasenwinkel oder der Zeit aufgetragen einen Sinusverlauf.
Die blau gezeichnete Schwingung läuft der rot gezeichneten um 60° vor.
Zu einer recht kompakten mathematischen Behandlung ist die komplexe Wechselstromrechnung entwickelt worden, in der reelle physikalische Größen formal durch komplexe Größen ersetzt werden; und werden durch in der komplexen Ebene rotierende Zeiger abgebildet.[5] Sie drehen sich mit konstanter Winkelgeschwindigkeit um den Koordinatenursprung. Ihre Längen repräsentieren die Amplituden; die Abstände der Pfeilspitzen von der reellen Achse stehen für die Augenblickswerte; sie ändern sich mit der Zeit sinusförmig.[6]
Formelzeichen komplexer Größen werden durch Unterstreichung gekennzeichnet:[7]
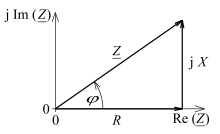
Auf der waagerechten Achse wird der Realteil der Impedanz aufgetragen, auf der senkrechten Achse der Imaginärteil.
Der Winkel in der Zeichnung entspricht dem Winkel im Text.
- und
mit der imaginären Einheit , die durch definiert wird. Ferner wird der komplexe Wechselstromwiderstand eingeführt, der auch Impedanz genannt wird:
Anders als beim Bruch kürzt sich beim Bruch die im Faktor enthaltene Zeitabhängigkeit heraus. Somit rotiert der zugehörige Zeiger nicht. Der komplexe Widerstand ermöglicht die Zusammenfassung von Wirk- und Blindwiderstand zu
und die Zusammenfassung von Scheinwiderstand und Phasenverschiebungswinkel zu
Davon wird nachfolgend Gebrauch gemacht.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, S. 316.
- ↑ Serge Lang: A First Course in Calculus. Fifth Edition. Springer, S. 59–61.
- ↑ Serge Lang: A First Course in Calculus. Fifth Edition. Springer, S. 83.
- ↑ Wilhelm Walcher: Praktikum der Physik. 6. Auflage, Teubner, 1989, Seite 243.
- ↑ Wilfried Weißgerber: Elektrotechnik für Ingenieure 2. Vieweg, 1991, Seite 5 ff.
- ↑ Ekbert Hering, Karl-Heinz Modler (Hrsg): Grundwissen des Ingenieurs. 14. Auflage. Fachbuchverlag Leipzig, 2007, Seite 167 ff.
- ↑ DIN 5483–3: Zeitabhängige Größen – Teil 3: Komplexe Darstellung sinusförmig zeitabhängiger Größen. Sept. 1994.

































































